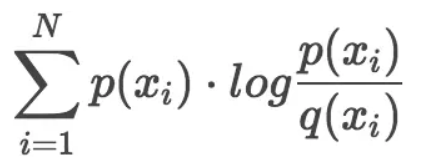信息熵
假设随机从口袋取硬币,口袋里有各一个蓝色的、红色的、绿色的、橘色的硬币。我们的目标是:问最少的问题,得到正确的答案。如下:
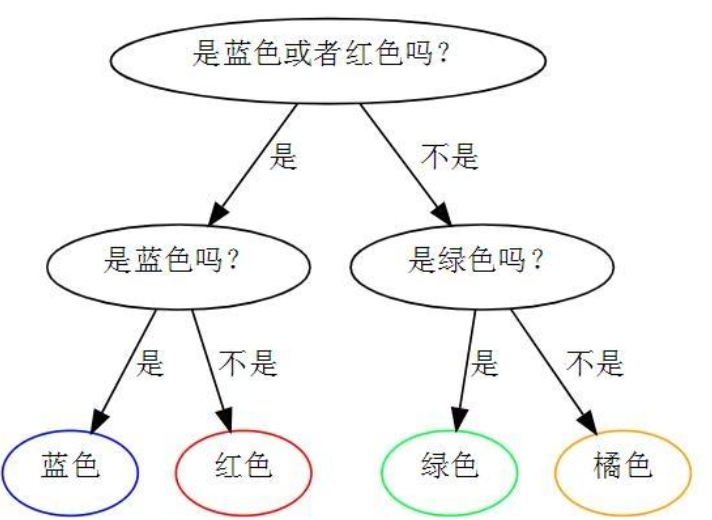
每个硬币都有1/4的概率被选中,1/4(概率)*2(问题个数)4(球的数量)=2。平均需要问两道题才能找出不同颜色的球,也就是说期望值是2,也叫做*信息熵。
如果改变一下上个例子,变成袋子中1/8的硬币是绿色的,1/8的是橘色的,1/4是红色的,1/2是蓝色的。
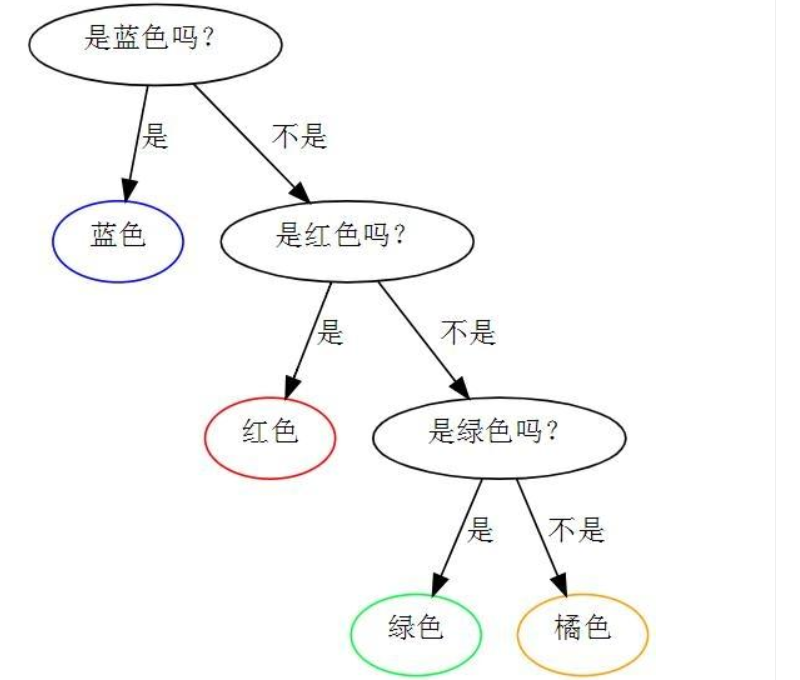
蓝色硬币概率为1/2,所以只需要一个问题就知道是还是不是蓝色,红色硬币概率为1/4,需要两个问题,以此类推,橘色和绿色硬币需要3个问题。所以,信息熵=期望=1/2x1+1/4x2+1/8x3+1/8x3=1.75
所以,问题个数的期望是:
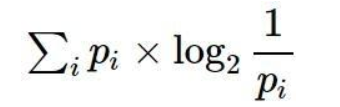
这个式子就是信息熵的表达式。也可以写作: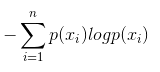
简单来说, 其意义就是在最优化策略下, 猜到颜色所需要的问题的个数。熵代表的是随机变量或整个系统的不确定性,信息熵越大,随机变量或系统的不确定性就越大。
联合熵
从信息熵公式可得,随机变量的取值个数越多,状态数也就越多,信息熵就越大,混乱程度就越大。
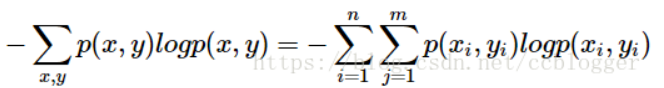
交叉熵
口袋还是1/8的硬币是绿色的,1/8的是橘色的,1/4是红色的,1/2是蓝色的,但是换一个策略:
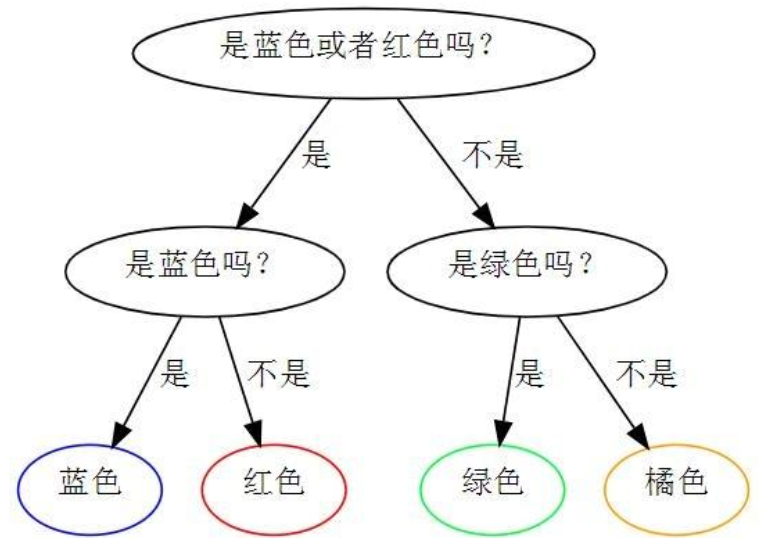
需要问的问题数=1/8x2+1/8x2+1/4x2+1/4x2=2。2就是这个策略的交叉熵,而最优策略的交叉熵是1.75。而1/8概率橘色硬币和1/2概率的蓝色硬币一样,都是需要两个问题得到颜色。也就是说,小球的分布为(1/4,1/4,1/4,1/4),这个分布就是非真实分布
给定一个策略,交叉熵就是在该策略下猜中颜色所需要的问题的期望值。交叉熵用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出成本的大小。交叉的字面意思在于:真实分布与非真实分布的交叉。给定一个方案,越优的策略,交叉熵越低,具有最低的交叉熵策略就是最优的策略。而在此时,交叉熵=信息熵。因此,我们通常需要最小化交叉熵,也间接证明了我们的算法所算出的非真实分布接近真实分布。交叉熵也叫对数似然
交叉熵公式:
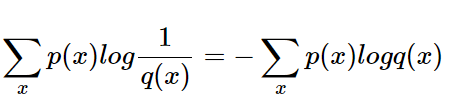
条件熵
条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。条件熵H(Y|X)定义为X给定条件下Y的条件概率分布的熵对X的数学期望。条件熵也被称为信息增益,信息增益越大,特征表现越好。
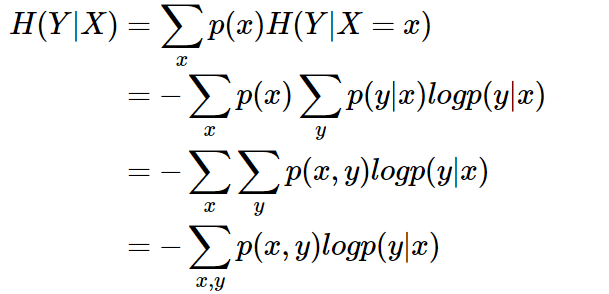
条件熵(Y|X)等于联合熵H(X,Y)减去单独的熵H(X),H(Y|X)=H(X,Y)-H(X)。
相对熵
相对熵又称为KL散度,它表示2个函数或概率分布的差异性:差异越大则相对熵越大,差异越小则相对熵越小。设p为概率分布,q为另一分布