优化算法（2）

Mini-batch 梯度下降

我们之前学过，向量化能够让我们有效地对所有m个样本进行计算，所以我们要把训练样本放到巨大的矩阵X中。

X=[x⁽¹⁾ x⁽²⁾ x⁽³⁾ x⁽⁴⁾ …… x⁽ⁿ⁾ ]。Y也是如此，Y=[y⁽¹⁾ y⁽²⁾ y⁽³⁾ y⁽⁴⁾ …… y⁽ⁿ⁾ ]。所以X的维度是(n_x,m)，Y的维度是(1,m)。向量化能够让我们相对较快地处理所有样本，如果m很大的话，处理速度仍然缓慢。

相比于mini-batch梯度下降法，我们大家更熟悉的应该是batch梯度下降法，即梯度下降法。那batch梯度下降法和mini-batch梯度下降法有什么区别吗？其实它俩的区别就存在于名字中，一个是batch，即进行梯度下降训练时，使用全部的训练集，而mini-batch，表示比batch小一些，就是指在进行梯度下降训练时，并不使用全部的训练集，只使用其中一部分数据集。

我们知道，不论是梯度下降法还是mini-batch梯度下降法，我们都可以通过向量化(vectorization)更加有效地计算所有样本。既然已经有了梯度下降法，我们为什么还要提出mini-batch梯度下降法呢？在实际计算中，我们可能会遇到特别大的数据集，这时再使用梯度下降法，每次迭代都要计算所有的数据集，计算量太大，效率低下，而mini-batch梯度下降法允许我们拿出一小部分数据集来运行梯度下降法，能够大大提高计算效率。

我们可以把训练集分割成小一点的子集训练，这些子集被取名为mini-batch，假设每一个子集中只要1000个样本，那么把x⁽¹⁾到x⁽¹⁰⁰⁰⁾取出来，将其称为第一个子训练集，也叫做mini-batch，然后我们再取出接下来的1000个样本，从x⁽¹⁰⁰¹⁾到x⁽²⁰⁰⁰⁾，然后再取1000个样本，以此类推。

接下来是吴恩达老师的一个新的符号，把x⁽¹⁾到x⁽¹⁰⁰⁰⁾称为X^{1}，x⁽¹⁰⁰¹⁾到x⁽²⁰⁰⁰⁾称为X^{2}，如果我们的训练样本一共有500万个，每个mini-batch都有1000个样本。也就是说，你有5000个mini-batch，因为5000乘以1000就是500万。最后得到的是X^{5000}，对y进行相同的处理。

mini-batch的数量t组成X^{t}和Y^{t}，这就是10000个训练样本。包括相应的输入输出对。如果X^{1}是一个有1000个样本的训练集，X^{1}的维度应该是(n_x,1000)，X^[2]的应该也是(n_x，1000)，以此类推，所有的子集维数都是(n_x,1000)，对于Y也是一样的。

之前我们执行前向传播，就是执行z^[1]=W^[1]X+b^[1]。变成mini-batch后呢，把X替换成X^[t]，即z^[1]=W^[1]X^{t}+b^[1]，然后执行A^[1]k=g^[1](Z^[1])，依次类推，直到A^[L]=g^[L](Z^[L])，这就是我们的预测值。注意：这里一次性处理的是1000个样本不是500万个样本。接着计算成本函数，因为子集规模是1000，所以J=1/1000$\sum_{i=1}^{1000}$L(y⁽ⁱ⁾ 帽,y⁽ⁱ⁾)。

如果我们使用了正则化，

你也会注意到，我们做的一切似曾相识，其实跟之前我们执行梯度下降法如出一辙，除了现在的对象不是X，Y，而是X^{t}和Y^{t}。接下来，执行反向传播来计算J^{t}的梯度，你只是使用X^{t}和Y^{t}，然后更新加权值，W实际上是W^[l]，更新为W^[l]=W^[l]-adW^[l]。对b做相同处理，b^[l]=b^[l]-adb^[l]。这是使用mini-batch梯度下降法训练样本的一步。被称为进行“一代”（1 epoch）的训练。一代这个词意味着只是遍历了一次训练集。我们可以在外围加一个for循环，从1到5000，因为我们有5000个各有1000个样本的组。

使用batch梯度下降法，一次遍历训练集只能让你做一个梯度下降，使用mini-batch梯度下降法，一次遍历训练集，能让你做5000个梯度下降。

理解mini-batch

使用batch梯度下降法时，每次迭代都需要历遍整个训练集，可以预期每次迭代成本都会下降，所以如果成本函数是迭代次数的一个函数，它应该会随着每次迭代而减少，如果在某次迭代中增加了，那肯定出了问题，也许学习率太大。

使用mini-batch梯度下降法，如果你作出成本函数在整个过程中的图，则并不是每次迭代都是下降的，特别是在每次迭代中，你要处理的是X^{t}和Y^{t}，如果要作出成本函数J^{t}的图，而J^{t}只和X^{t}，Y^{t}有关，也就是每次迭代下你都在训练不同的样本集或者说训练不同的mini-batch。

我们需要决定的变量之一是mini-batch的大小，m就是训练集的大小。其中一个极端情况下，mini-batch梯度下降法就是batch梯度下降法。另一个极端情况，假设mini-batch大小为1，就有了新的算法，叫做随机梯度下降法，每个样本都是独立的mini-batch，当你看第一个mini-batch，也就是X^{1}和Y^{1}，如果mini-batch大小为1，它就是你的第一个训练样本。接着再看第二个mini-batch，也就是第二个训练样本，采取梯度下降步骤，然后是第三个训练样本，以此类推，一次只处理一个。

实际上你选择的mini-batch大小在二者之间，大小在1和m之间，而1太小了，m太大了。如果取n，每个迭代需要处理大量训练样本，单次迭代耗时太长。如果训练样本不大，batch梯度下降法运行地很好。相反，如果使用随机梯度下降法，如果你只要处理一个样本，那这个方法很好，这样做没有问题，通过减小学习率，噪声会被改善或有所减小，但随机梯度下降法的一大缺点是，你会失去所有向量化带给你的加速，因为一次性只处理了一个训练样本，这样效率过于低下，所以实践中最好选择不大不小的mini-batch尺寸，实际上学习率达到最快。

首先，如果训练集较小，直接使用batch梯度下降法，样本集较小就没必要使用mini-batch梯度下降法，可以快速处理整个训练集，所以使用batch梯度下降法也很好，这里的少是说小于2000个样本，这样比较适合使用batch梯度下降法。不然，样本数目较大的话，一般的mini-batch大小为64到512，考虑到电脑内存设置和使用的方式，如果mini-batch大小是2的n次方，代码会运行地快一些，64就是2的6次方，以此类推，128是2的7次方，256是2的8次方，512是2的9次方。所以我经常把mini-batch大小设成2的次方。

最后需要注意的是在你的mini-batch中，要确保X^{t}和Y^{t}要符合CPU/GPU内存，取决于你的应用方向以及训练集的大小。如果不符合内存，无论采取什么方法处理数据，结果变得惨不忍睹。

指数加权平均数

指数加权平均也叫指数加权移动平均，是一种常用的序列数据处理方式。

它的计算公式是：

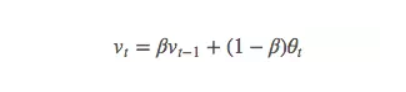
其中，

• θ_t：为第 t 天的实际观察值，
• V_t: 是要代替 θ_t 的估计值，也就是第 t 天的指数加权平均值，
• β： 为 V_{t-1} 的权重，是可调节的超参。( 0 < β < 1 )

下面是一组气温数据，图中横轴为一年中的第几天，纵轴为气温：

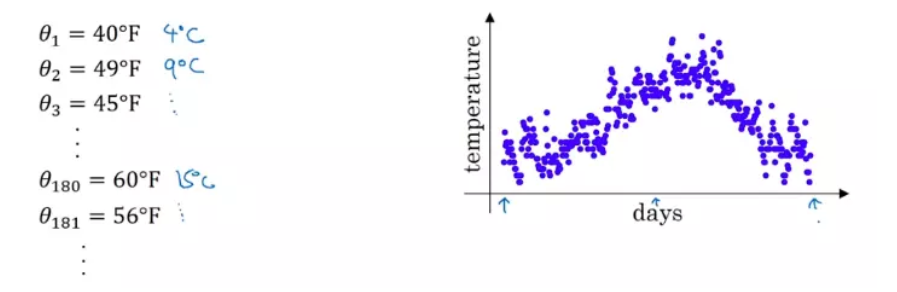
直接看上面的数据图会发现噪音很多，

这时，我们可以用 指数加权平均 来提取这组数据的趋势，

按照前面的公式计算：

这里先设置 β = 0.9，首先初始化 V_0 ＝ 0，然后计算出每个 V_t，将计算后得到的V_t表示出来，得到下图红色线：

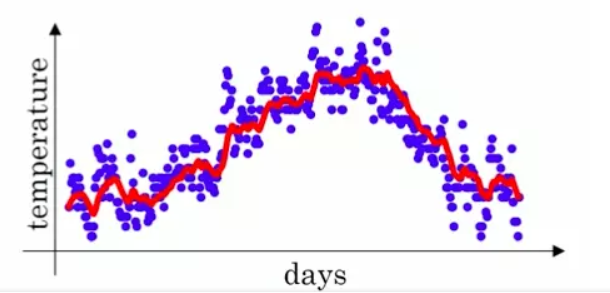
可以看出，红色的数据比蓝色的原数据更加平滑，少了很多噪音，并且刻画了原数据的趋势。

指数加权平均，作为原数据的估计值，不仅可以 1. 抚平短期波动，起到了平滑的作用，2. 还能够将长线趋势或周期趋势显现出来。

我们可以改变β值，当β=0.98时，得出下图的绿线。当β=0.5，结果是下图的黄线。

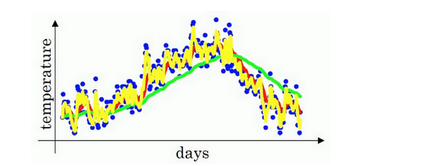
理解指数加权平均数

上个小节，我们得出下面公式。

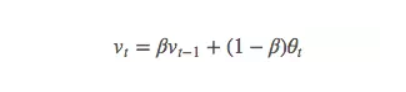
我们进一步分析，来理解如何计算出每日温度的平均值

使β=0.9，得出下面公式：

将第二个公式带到第一个，第三个公式带到第二个公式，一次类推，把这些展开：

我们可以将v₀，v₁，v₂等等写成明确的变量，不过在实际中执行的话，你要做的是，一开始将v₀初始化为0，然后在第一天使v=βv+(1-β)θ₁，然后第二天，更新v值，v=βv+(1-β)θ₂，以此类推，有些人会把v加下标，来表示v是用来计算数据的指数加权平均数。

指数加权平均数公式的好处之一在于，它占用极少内存，电脑内存中只占用一行数字而已，然后把最新数据代入公式，不断覆盖就可以了。

指数加权平均的偏差修正

偏差修正可以让平均数运算更加准确

在前几节中，如上图，红色曲线对应β为0.9，绿色曲线对应的β=0.98。吴恩达老师说执行下面这个公式：

v_t=βv_t-1+(1-β)θ_t

得到的就是紫色曲线，而不是绿色曲线。后面紫色和绿色有大部分重合。PS：为什么？同时0.98，紫色曲线的起点低。

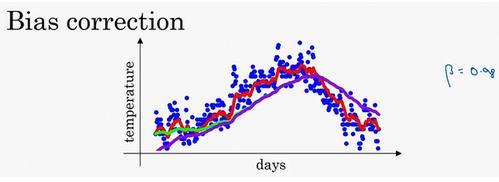
计算移动平均数时，初始化v₀，v₁=0.98v₀+0.02θ₁，因为v₀=0，所以0.98v₀=0。所以v₁=0.02θ₁，如果第一天温度时40，v₁=0.02 x 40=8。因此得到的值会小很多，所以第一天的温度估测不准。

v₁=0.98v₀+0.02θ₁，如果带入v₁，然后相乘，v₂=0.98 x 0.02θ₁ + 0.02θ₂，假如θ₁和θ₂都是正数，计算后的v₂要远小于θ₂和θ₁，所以不能很好预估这一年前两天的温度。

有个办法可以修改这一估测，让估测变得更好，更准确，特别是在估测初期，也就是不用v_t，而是用v_t/1-β^t，t就是现在的天数。举个具体例子，当t=2时，1-β^t=1-0.98²=0.0396，因此对第二天温度的估测变成了

v₂/0.0396=(0.0196θ₁+0.02θ₂)/0.0396

也就是和的加权平均数，并去除了偏差。你会发现随着t增加，β^t接近于0，所以当t很大的时候，偏差修正几乎没有作用.因此当t较大的时候，紫线基本和绿线重合了。不过在开始学习阶段，你才开始预测热身练习，偏差修正可以帮助你更好预测温度，偏差修正可以帮助你使结果从紫线变成绿线。

动量梯度下降法

还有一种算法叫做Momentum，或者叫做动量梯度下降法，运行速度几乎总是快于标准的梯度下降算法。基本的想法就是计算梯度的指数加权平均数，并利用该梯度更新的权重。

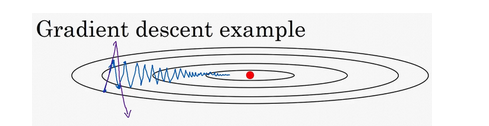
如果优化成本函数，函数形状如图，红点代表最小值的位置，假设从这里（蓝色点）开始梯度下降法，如果进行梯度下降法的一次迭代，无论是batch或mini-batch下降法，也许会指向这里，现在在椭圆的另一边，计算下一步梯度下降，结果或许如此，然后再计算一步，再一步，计算下去。我们发现梯度下降法要很多计算步骤。

慢慢摆动到最小值，这种上下波动减慢了梯度下降法的速度，就无法使用更大的学习率，如果要用较大的学习率（紫色箭头），结果可能会偏离函数的范围，为了避免摆动过大，就要用一个较小的学习率。

另一个看待问题的角度是，在竖直方向上，我们希望学习慢一点，因为我们不想要这些摆动。但在水平方向，我们希望快速从左向右移动，移向最小值，移向红点。所以使用动力梯度下降法，在每次迭代中，都会计算dW，db。我们要做的是计算v_dW=βv_dW+(1-β)dW，接着同样计算v_db=βv_db+(1-β)db。然后重新赋值权重，W=W-av_dW，同样b=b-av_dW，从而减缓梯度下降的幅度。

举个例子，如果你站在一个地方不动，让你立刻向后转齐步走，你可以迅速向后转然后就向相反的方向走了起来，批梯度下降和随机梯度下降就是这样，某一时刻的梯度只与这一时刻有关，改变方向可以做到立刻就变。而如果你正在按照某个速度向前跑，再让你立刻向后转，可以想象得到吧，此时你无法立刻将速度降为0然后改变方向，你由于之前的速度的作用，有可能会慢慢减速然后转一个弯。

动量梯度下降是同理的，每一次梯度下降都会有一个之前的速度的作用，如果我这次的方向与之前相同，则会因为之前的速度继续加速；如果这次的方向与之前相反，则会由于之前存在速度的作用不会产生一个急转弯，而是尽量把路线向一条直线拉过去。

这就解决了文中第一个图的那个在普通梯度下降中存在的下降路线折来折去浪费时间的问题。

我们有两个超参数，学习率α以及β参数。β是指数加权平均数，常用值为0.9。

RMSprop

前面我们知道动力梯度下降法可以加快梯度下降，还有一个叫做RMSprop的算法，全称是root mean square prop算法，它也可以加速梯度下降，我们来看看它是如何运作的。

复习前面的内容，如果我们执行梯度下降，虽然横轴方向正在推进，但纵轴方向会有大幅动摆动。所以，我们想减缓纵轴方向的学习，同时加快横轴方向的学习(至少不减慢)。RMSprop算法可以实现这个目标。

在第t次迭代中，该算法会找出计算mini-batch的微分dW，db。这里我们不用v_dW，而是用到新符号S_dW。因此：

S_dW=βS_dW+(1-β)(dW)²，这里的平方是对整个dW平方。

S_db=βS_db+(1-β)db²，这里的平方也是对整个db平方。

接着，RMSprop会更新参数值。如下：

我们希望，S_dW相对较少，S_db较大。因为垂直方向的微分要比水平方向的大得多，所以斜率在垂直方向特别大。所以db较大，dW较小。db的平方较大，所以S_db的平方较大。dW会小，S_dW也会小。结果就是纵轴上的更新要被一个较大的数相除，就能消除摆动，而水平方向的更新则被较小的数相除。

RMSprop的影响就是你的更新最后会变成这样（绿色线），纵轴方向上摆动较小，而横轴方向继续推进。还有个影响就是，你可以用一个更大学习率a，然后加快学习，而无须在纵轴上垂直方向偏离。

Adam优化算法

Adam优化算法基本上就是将Momentum和RMSprop结合在一起，那么来看看如何使用Adam算法。

首先，初始化

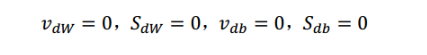
然后用当前的 mini-batch 计算出 dW 和 db

接下来计算 Momentum 指数加权平均数：

上图中用到的β₁是为了和下面的RMSprop公式中用到的β₂相互区分

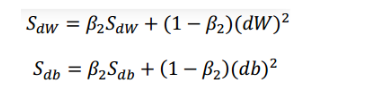
一般运用 Adam 算法的时候，我们还要对 v 和 S 的偏差进行修正：

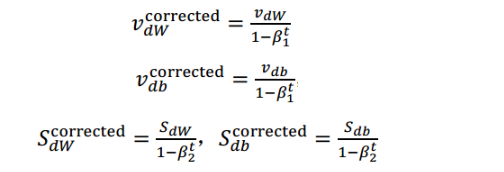
然后就是权重的更新：

完整的如下所示：

本算法有很多超参数，分别有a、β₁、β₂、ξ四个超参数。a需要调试，尝试一系列的值，然后看哪个有效。β₁常用的值为0.9。至于β₂，推荐使用0.999，ξ为10^-8。

学习率衰减

加快学习算法的一个办法就是随时间慢慢减少学习率，我们将之称为学习率衰减。

假设使用mini-batch梯度下降法，mini-batch数量不大，大概64或者128个样本，在迭代过程中会有噪音（蓝色线），下降朝向这里的最小值，但是不会精确地收敛，所以你的算法最后在附近摆动，并不会真正收敛，因为你用的a是固定值，不同的mini-batch中有噪音。

但是如果要减少学习率的话，在初期的时候，a学习率还比较大，我们的学习还是相对较快，但随着a变小，我们的步伐也会变慢。而不是在训练过程中，大幅度在最小值附近摆动。

所以慢慢减少a的本质在于，在学习初期，承受较大的步伐，但当开始收敛的时候，小一些的学习率能让你步伐小一些。

我们应该拆分成不同的mini-batch。第一次遍历训练集叫做第一代，第二代就是第二代。以此类推，我们得出公式：

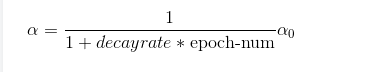
decay-rate称为衰减率，epoch-num为代数，α₀为初始学习率），注意这个衰减率是另一个你需要调整的超参数。

当然还有其它衰减：

方法二：指数衰减

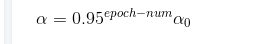
方法三：

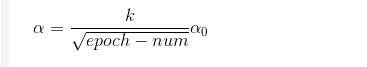
方法四：

方法五：手动衰减

如果一次只训练一个模型，如果花上数小时或数天来训练，看看自己的模型训练，耗上数日，学习速率变慢了，然后把α调小一点。但这种方法只是在模型数量小的时候有用。

局部最优

也许我们想优化一些参数，我们把它们称之为W₁和W₂，平面的高度就是损失函数。在图中似乎各处都分布着局部最优。梯度下降法或者某个算法可能困在一个局部最优中，而不会抵达全局最优。如果要作图计算一个数字，比如说这两个维度，就容易出现有多个不同局部最优的图，而这些低维的图曾经影响了我们的理解，但是这些理解并不正确。事实上，如果你要创建一个神经网络，通常梯度为零的点并不是这个图中的局部最优点，实际上成本函数的零梯度点，通常是鞍点。

在高维度空间，我们更可能碰到鞍点。

首先，你不太可能困在极差的局部最优中，条件是你在训练较大的神经网络，存在大量参数，并且成本函数J被定义在较高的维度空间。

第二点，平稳段是一个问题，这样使得学习十分缓慢，这也是像Momentum或是RMSprop，Adam这样的算法，能够加速学习算法的地方。在这些情况下，更成熟的优化算法，如Adam算法，能够加快速度，让你尽早往下走出平稳段。

名词解释：平稳段是一段区域，其中导数长时间接近于0。