人脸验证和神经风格转换

One—Shot学习

人脸识别所面临的一个挑战就是需要解决一次学习问题，这意味着在大多数人脸识别应用中，需要通过单单一张图片或者单单一个人脸样例就能去识别这个人。而在我们的学习过程中，发现深度学习只有一个训练样例时，它的表现并不好。接下来解决一下这个问题。

假设我们的数据库有以下四张照片：

有一种办法是，将人的照片放进卷积神经网络中，使用softmax单元来输出4种，或者说5种标签，分别对应这4个人，或者4个都不是，所以softmax里我们会有5种输出。但实际上这样效果并不好，因为如此小的训练集不足以去训练一个稳健的神经网络。而且，假如有新人加入团队，我们现在将会有5个组员需要识别，所以输出就变成了6种，这时你要重新训练神经网络吗？这听起来实在不像一个好办法。

所以要让人脸识别能够做到一次学习，为了能有更好的效果，现在要做的应该是学习Similarity函数。详细地说，想要神经网络学习这样一个用d表示的函数：d(img1,img2)=degree of difference between images。

它以两张图片作为输入，然后输出这两张图片的差异值。如果你放进同一个人的两张照片，你希望它能输出一个很小的值，如果放进两个长相差别很大的人的照片，它就输出一个很大的值。所以在识别过程中，如果这两张图片的差异值小于某个阈值τ，它是一个超参数，那么这时就能预测这两张图片是同一个人，如果差异值大于τ，就能预测这是不同的两个人，这就是解决人脸验证问题的一个可行办法。

Siamese网络

通过上一小节我们知道我们该怎么去做人脸识别，通过输入两张图片。它将让你解决一次学习问题。接下来我们学习如何训练我们的神经网络学会这个函数d。

看上图，我们经常看到这样的卷积网络，输入图片，然后通过一些列卷积，池化和全连接层，最终得到编号1这样的特征向量。有时这个会被送进softmax单元来做分类。但是我们关注的重点是编号1，假如它有128个数，它是由网络深层的全连接层计算出来的，我们要给这128个数命个名字，把它叫做f(x⁽¹⁾)。可以把f(x(⁽¹⁾)看作是输入图像x⁽¹⁾的编码，取这个输入图像（编号2），然后表示成128维的向量。

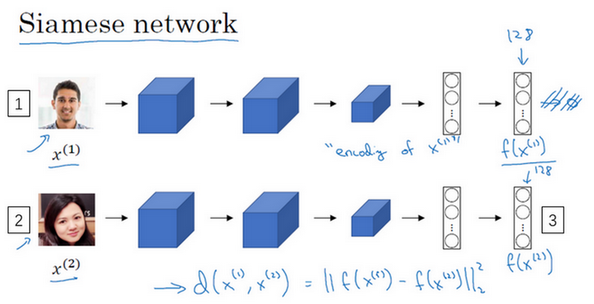
建立一个人脸识别系统的方法就是，如果你要比较两个图片的话，例如这里的第一张（编号1）和第二张图片（编号2），你要做的就是把第二张图片喂给有同样参数的同样的神经网络，然后得到一个不同的128维的向量（编号3），这个向量代表或者编码第二个图片，我们把第二张图片的编码叫做f(x⁽²⁾)。这里我用x⁽¹⁾和x⁽²⁾仅仅代表两个输入图片，它们没必要非是第一个和第二个训练样本，可以是任意两个图片。最后如果相信这些编码很好地代表了这两个图片，我们要做的就是定义d，将x⁽¹⁾和x⁽²⁾的距离定义为这两幅图片的编码之差的范数。

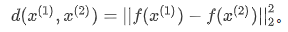
那么怎么训练这个Siamese神经网络呢？不要忘了这两个网络有相同的参数，所以实际要做的就是训练一个网络，它计算得到的编码可以用于函数d，它可以告诉我们两张图片是否是同一个人。更准确地说，神经网络的参数定义了一个编码函数，如果给定输入图像，这个网络会输出的128维的编码。你要做的就是学习参数，使得如果两个图片和是同一个人，那么你得到的两个编码的距离就小。相反，如果和是不同的人，那么我们会想让它们之间的编码距离大一点。

训练神经网络

训练神经网络两种方法：Triplet 损失和人脸识别二分类

Triplet损失

要想学习神经网络参数来得到优质的人脸图片编码，方法之一就是定义三元组损失函数然后应用梯度下降。看到这个的时候，我也一脸懵逼。这是什么啊？接下来我们一起看下。

我们看下这是什么意思，为了应用三元组损失函数，你需要比较成对的图像，比如这个图片，为了学习网络的参数，你需要同时看几幅图片，比如这对图片（编号1和编号2），你想要它们的编码相似，因为这是同一个人。然而假如是这对图片（编号3和编号4），你会想要它们的编码差异大一些，因为这是不同的人。

用三元组损失的术语来说，我们要做的通常是看一个 Anchor 图片，想让Anchor图片和Positive图片（Positive意味着是同一个人）的距离很接近。然而，当Anchor图片与Negative图片（Negative意味着是非同一个人）对比时，我们会想让他们的距离离得更远一点。

这就是为什么叫做三元组损失，它代表你通常会同时看三张图片，你需要看Anchor图片、Postive图片，还有Negative图片，我要把Anchor图片、Positive图片和Negative图片简写成A、P、N。

把以上内容写成公式的话，d= ||f(A)-f(P)||²。我们希望||f(A)-f(P)||² <= ||f(A)-f(N)||²。||f(A)-f(P)||² 就是d(A,P)，||f(A)-f(N)||²时d(A,N)，我们可以把d看为距离函数。

对表达式修改一下，因为有一种情况满足这个表达式，但是没有用处，就是把所有的东西都学成0，如果总是输出0，即0-0≤0，这就是0减去0还等于0，如果所有图像的都是一个零向量，那么总能满足这个方程f。所以为了确保网络对于所有的编码不会总是输出0，也为了确保它不会把所有的编码都设成互相相等的。另一种方法能让网络得到这种没用的输出，就是如果每个图片的编码和其他图片一样，这种情况，还是得到0-0。

为了阻止网络出现上述状况，我们需要修改表达式。也就是||f(A)-f(P)||² - ||f(A)-f(N)||²不能刚好小于等于0。应该是比0还要小，所以这个应该小于一个-a，也就是||f(A)-f(P)||² - ||f(A)-f(N)||² <= -a。这里的a是一个超参数，是为了阻止网络输出无用的结果。

举个例子，假如间隔设置成0.2，如果在这个例子中，d(A,P)=0.5，如果 Anchor和 Negative图片的，即只大一点，比如说0.51，条件就不能满足。虽然0.51也是大于0.5的，但还是不够好，我们想要比大很多。你会想让这个值d(A,N)至少是0.7或者更高，这样间距至少达到0.2，你可以把这项调大或者这个调小。超参数a至少是0.2，在d(A,P)和d(A,N)之间至少相差0.2，这就是间隔参数的作用。

接下来定义损失函数。

这个max函数的作用就是，只要这个||f(A)-f(P)||² - ||f(A)-f(N)||²+a <= 0，那么损失函数就是0。另一方面如果||f(A)-f(P)||² - ||f(A)-f(N)||²+a>=0，然后取最大值。最后得到||f(A)-f(P)||² - ||f(A)-f(N)||²+a，这样就会得到一个正的损失值。通过最小化这个损失函数达到的效果就是使这部分||f(A)-f(P)||² - ||f(A)-f(N)||²+a小于等于0，只要这个损失函数小于等于0，网络不会关心它负值有多大。

这是一个三元组定义的损失，整个网络的代价函数应该是训练集中这些单个三元组损失的总和。假如你有一个10000个图片的训练集，里面是1000个不同的人的照片，你要做的就是取这10000个图片，然后生成这样的三元组，然后训练你的学习算法，对这种代价函数用梯度下降，这个代价函数就是定义在你数据集里的这样的三元组图片上。

注意，为了定义三元组的数据集你需要成对的A和P，即同一个人的成对的图片，为了训练你的系统你确实需要一个数据集，里面有同一个人的多个照片。这也是为什么在这个例子中，我说假设你有1000个不同的人的10000张照片，也许是这1000个人平均每个人10张照片，组成了你整个数据集。如果你只有每个人一张照片，那么根本没法训练这个系统。当然，训练完这个系统之后，你可以应用到你的一次学习问题上，对于你的人脸识别系统，可能你只有想要识别的某个人的一张照片。但对于训练集，你需要确保有同一个人的多个图片，至少是你训练集里的一部分人，这样就有成对的Anchor和Positive图片了。

那么我们该怎么选择这些三元组来形成训练集呢？一个问题是如果从训练集中，随机地选择A、P和N，遵守A和P是同一个人，而 A 和 N 是不同的人这一原则。有个问题就是，如果随机的选择它们，那么这个约束条件 d(A,P)+a<=d(A,N) 很容易达到，因为随机选择的图片，A和N 比 A和P差别很大的概率很大。所以有很大的可能性|| f(A)-f(N) ||会比||(f(A) -f(P) )||大，而且差距远大于a，这样网络并不能从中学到什么。

所以为了构建一个数据集，要做的就是尽可能选择难训练的三元组A、P和N。具体而言，你想要所有的三元组都满足这个条件 d(A,P)+a<=d(A,N)。难训练的三元组就是，你的A、P和N的选择使得很接近，即d(A,P)约等于d(A,N)。这样的学习算法会竭尽全力使d(A,N)式子变大，或者使d(A,P)变小，这样左右两边至少有一个的间隔。并且选择这样的三元组还可以增加你的学习算法的计算效率，如果随机的选择这些三元组，其中有太多会很简单，梯度算法不会有什么效果，因为网络总是很容易就得到了正确的结果，只有选择难的三元组梯度下降法才能发挥作用，使得这两边离得尽可能远。

人脸验证与二分类

上述的Triplet loss是一个学习人脸识别卷积网络参数的好方法。另一个训练神经网络的方法是选取一对神经网络Siamese网络，使其同时计算这些嵌入，比如说128维的嵌入（编号1），或者更高维，然后将其输入到逻辑回归单元，然后进行预测，如果是相同的人，那么输出是1，若是不同的人，输出是0。这就把人脸识别问题转换为一个二分类问题，训练这种系统时可以替换Triplet loss的方法。

最后的逻辑回归单元输出 y帽：

f(x⁽ⁱ⁾)_k 代表图片x⁽ⁱ⁾ 的编码，下标 k代表选择这个向量中的第k个元素。| f(x⁽ⁱ⁾)_k -f(x⁽ⁱ⁾)_k |是对着两个编码取元素差的绝对值。把这128个元素当作特征，然后把他们放入逻辑回归中，最后的逻辑回归可以增加参数ω_i 和 b，就像普通的逻辑回归一样。你将在这128个单元上训练合适的权重，用来预测两张图片是否是一个人，这是一个很合理的方法来学习预测0或者1，即是否是同一个人。

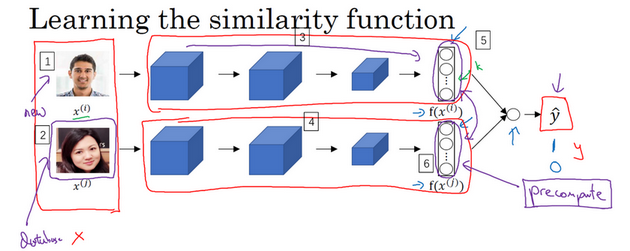
但是在这个学习公式中，输入是一对图片，这是你的训练输入x（编号1、2），输出y是0或者1，取决于你的输入是相似图片还是非相似图片。与之前类似，你正在训练一个Siamese网络，意味着上面这个神经网络拥有的参数和下面神经网络的相同（编号3和4所示的网络），两组参数是绑定的，这样的系统效果很好。

如果这是一张新图片（编号1），当员工走进门时，希望门可以自动为他们打开，这个（编号2）是在数据库中的图片，不需要每次都计算这些特征（编号6），不需要每次都计算这个嵌入，你可以提前计算好，那么当一个新员工走近时，你可以使用上方的卷积网络来计算这些编码（编号5），然后使用它，和预先计算好的编码进行比较，然后输出预测值。因此不需要存储原始图像，如果你有一个很大的员工数据库，你不需要为每个员工每次都计算这些编码。这个预先计算的思想，可以节省大量的计算。