经典网络
LeNet - 5
LeNet-5是专门为灰度图训练的。所以他的图像样本的深度都是1。
LeNet-5的网络结构:

AlexNet
网络结构:

实际上论文的原文是使用224x224x3的,但经过试验发现227x227x3效果更好。
VGG-16
网络结构:
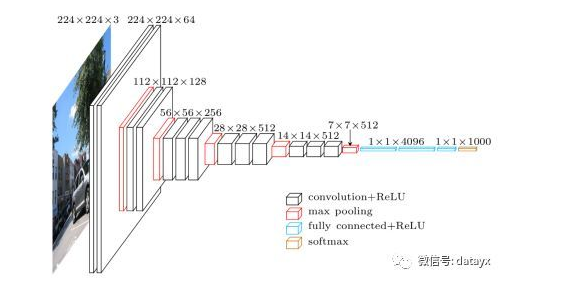
从左至右,一张彩色图片输入到网络,白色框是卷积层,红色是池化,蓝色是全连接层,棕色框是预测层。预测层的作用是将全连接层输出的信息转化为相应的类别概率,而起到分类作用。
可以看到 VGG16 是13个卷积层+3个全连接层叠加而成。
残差网络
网络越深越难训练,因为存在梯度消失和梯度爆炸的问题。本小节学习跳远连接。跳远连接可从某一个网络层激活,然后迅速反馈给另外一层甚至是神经网络的更深层。我们可以利用跳远连接构建能够训练深度网络的ResNets。
ResNets是由残差块构建的。那什么是残差块?看下图

这是一个两层的神经网络,它在L层进行激活,得到a[ l +1]再次进行激活,两层之后得到a[ l +2]。下图中的黑色部分即为计算过程。

而在残差网络中,我们直接将a^[ l ]拷贝到蓝色箭头所指位置。在线性激活之后、Relu非线性激活之前加上a[ l ],不在沿着原来的主路径传递。这就意味者我们主路径过程的第四个式子替换为蓝色式子,也正是这个蓝色式子中加上的a[ l ]产生了一个残差块。
为什么残差网络有用?
一个网络深度越深,它在训练集上训练网络的效率会有所减弱,但对于ResNets就不完全是这样了。
上一张图已经说过a^[ l +2]=g(z^[ l +2]+a^[ l ]),添加项a^[ l ]是刚添加的跳远连接的输入。解开这个式子,得:
a^[ l+2]=g(w^[ l+2] * a^[ l+1]+b^[ l+2]+a^[ l ]),这里w和b为关键值。如果w和b均为0,那a^[ l+2]=g(a^[ l ])=a^[ l ](假设这里得激活函数是Relu)。结果表明,残差块学习这个恒等式函数残差块并不难,跳远连接让我们很容易的得到a^[ l+2]=a^[ l ]
这意味着,即使给神经网络增加了这两层,它的效率也并不逊色于更简单的神经网络。因为对它来说,学习恒等函数对它来说很简单,尽管它多了两层,也只是把a^[ l ]的值赋给a^[ l+2]。
所以,残差网络有用的原因是这些函数残差块学习恒等函数非常容易。
1x1的卷积
看到这个标题,你也许会迷惑,1x1的卷积能做什么呢?不就是乘以数字吗?结果并非如此

看上图,你会觉得这个1x1的过滤器没什么用,只是对输入矩阵乘以某个数字。但这个1x1的过滤器仅仅是对于6x6x1的信道图片效果不好 。如果是一张6x6x32的图片就不一样了。
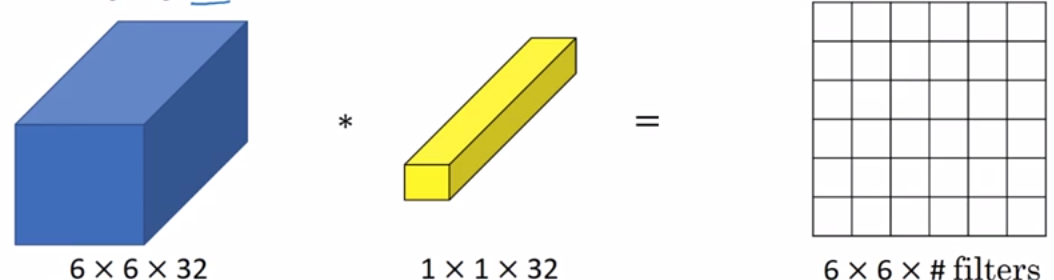
具体来说,1x1卷积所实现的功能是遍历这36个单元格。计算输入图中32个数字和过滤器中32个数字的乘积,然后应用Relu函数。我们以一个单元格为例,用着36个数字乘以这个输入层上1x1的切片,得到一个实数画在下面图中。
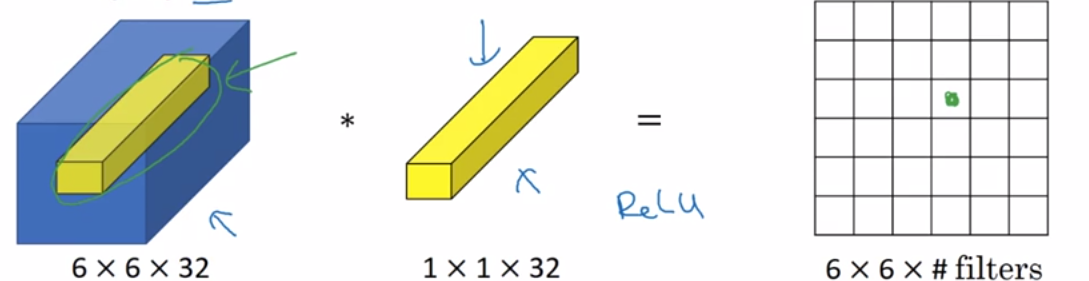
这个1x1x32的过滤器中的32可以这样理解,一个神经元的输入是32个数字,乘以相同高度和宽度上某个切片上的32个数字。这三十二个数字具有不同信道,乘以32个权重,然后应用Relu非线性函数。一般来说,如果过滤器不止一个,就好像有多个输入单元,其输入内容为一个切片上所有数字,输出结果是6x6x过滤器数量。所以1x1卷积可以从根本上理解为这32个单元都应用了一个全连接神经网络。全连接层的作用是输入32个数字和过滤器数量,标记为nc^[ l+1]。在36个单元上重复此过程,输出结果是6x6x过滤器数量。这种方法通常称为1x1卷积,也成为Network in Network。
下面是一个1x1卷积的应用:

假设这是一个28x28x192的输入层,我们可以利用池化层压缩它的高度和宽度。但是如果信道数量很大,我们该如何把它压缩为28x28x32维度的层呢?我们可以用32个大小为1x1的过滤器,每个过滤器的大小都是1x1x192维,因为过滤器中信道的数量必须与输入层中信道的数量一致。因此过滤器数量为32,输出层为28x28x32。这就是压缩nc的方法。
Inception网络
构建卷积层是,我们需要决定过滤器的大小是3x3还是5x5或者其它大小?或者要不要添加池化层?而我们接下来要讲的Inception就是代替我们来做决定的。虽然网络结构会变得非常复杂,但网络表现得非常好。我们来看一下原理。
基本思想:不需要人为的决定使用哪个过滤器,或者是否需要池化,而是由网络自行确定这些参数。人们只需给出这些参数的所有可能值,然后把这些输出连起来,让网络自己学习它需要什么样的参数,采用哪些过滤器组合。
举个例子:

如果我们直接计算上图,我们的计算成本为28x28x32x5x5x192
但是我们用1x1卷积后:

我们的计算成本变为28x28x16x192+28x28x32x5x5x16,使用1x1卷积后计算成本是没使用前的1/10。
下面再举一个例子:
例如:上一层的输出为100x100x128,经过具有256个输出的5x5卷积层之后(stride=1,pad=”SAME”),输出数据的大小为100x100x256。其中,卷积层的参数为5x5x128x256。假如上一层输出先经过具有32个输出的1x1卷积层,这时得图片输出为100x100x32,接着再经过具有256个输出的5x5卷积层,那么最终的输出数据的大小仍为100x100x256,但卷积参数量已经减少为1x1x128x32 + 5x5x32x256,大约减少了4倍。
在inception结构中,大量采用了1x1的矩阵,主要是两点作用:1)对数据进行降维;2)引入更多的非线性,提高泛化能力,因为卷积后要经过ReLU激活函数。
搭建inception网络:

inception就是将这些模块都组合到一起。
Inception network:
下面这个图就是Inception的网络:

看起来很复杂,但我们截取其中一个环节,如上图的红色框。就会发现这不正是我们搭建的inception吗。另外,再一些inception模块前网络会使用最大池化层来修改高和宽的维度。
其实上图的Inception并不完整,看下图:
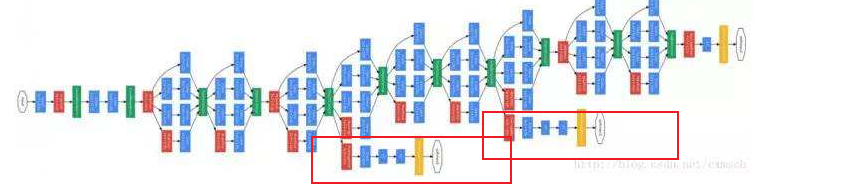
多出了红色框住的部分。这些分支是做什么的呢?这些分支是通过隐藏层做出预测。
迁移学习
我们在做计算机视觉的应用时,相对于从头训练权重,下载别人训练好的网络结构的权重作为我们预训练,然后转换到感兴趣的任务上。别人的训练过程可能是需要花费好几周,并且需要很多的GPU找最优的过程,这就意味着我们可以下载别人开源的权重参数并把它当做一个很好的初始化,用在我们的神经网络上。这就是迁移学习。

假如我们在做一个识别任务,却没有很多的训练集。我们就可以把别人的网络下载,冻结所有层的参数。我们只需要训练和我们Softmax层有关的参数,然后把别人Softmax改成我们自己Softmax。通过别人的训练的权重,我们可能会得到一个好的结果,即使我们的训练集并不多。
由于前面的层都冻结了,相当于一个固定函数,不需要改变,因为我们不训练它。
网络层数越多,需要冻结的层数越少,需要训练的层数就越多。
数据扩充
数据扩充也叫数据增强。因为计算机视觉相对于机器学习,数据较少。所以数据增强为了增加数据的数量。下面我们讲一下数据增强的办法:
垂直镜像对称
随机裁剪

色彩转换
给RGB三个通道加上不同的失真值

这些可以轻易改变图像的颜色,但是对目标的识别还是保持不变的。所以使用这种数据增强方法使得模型对照片的颜色更改更具鲁棒性。

