Python实现浅层神经网络

发表于 更新于 分类于

开始前的准备

本文用到的库：numpy、sklearn、matplotlib

另外，我们还要借助一下吴恩达老师的工具函数testCases.py 和 planar_utils.py。地址)

​ testCases：提供测试样本来评估我们的模型。

​ planar_utils：提供各种有用的函数。

这两个文件的函数就不具体阐述了，有兴趣的自己研究去吧。

导入必要的库

1
2
3
4
5
6
7
import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets

数据集介绍

1
2
#X是训练集，Y是测试集
X,Y=load_planar_dataset()

数据集的说明：

  • X是维度为(2, 400)的训练集，两个维度分别代表平面的两个坐标。
  • Y是为(1, 400)的测试集，每个元素的值是0（代表红色），或者1（代表蓝色）

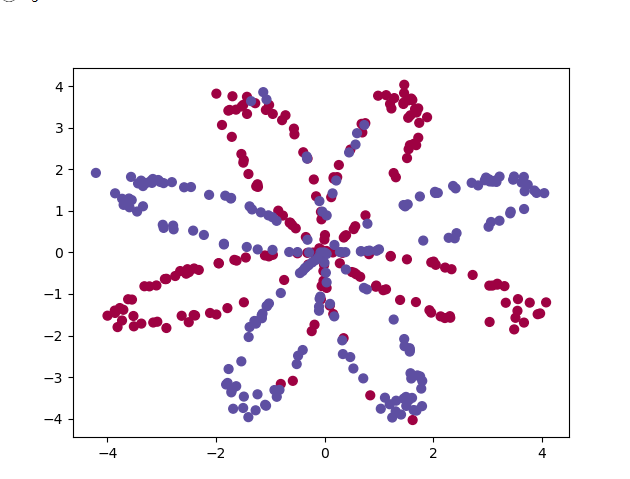
利用 matplotlib 进行数据的可视化操作，这是一个由红点和蓝色的点构成的类似花状的图像

1
2
3
4
5
    # np.squeeze()函数对矩阵进行压缩维度，删除单维度条目，即把shape中为1的维度去掉
    # 例如： np.squeeze([[ 1.23 ]]) 可以将维度压缩，最终变成 1.23
    # 目的是确保 cost 是一个浮点数
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral);
plt.show()

构建神经网络模型

对于某个样本x^[i]：

成本函数J：

接下来我们要用代码实现神经网络的结构，步骤大致如下： 1. 定义神经网络结构 2. 随机初始化参数 3. 不断迭代: - 正向传播 - 计算成本函数值 - 利用反向传播得到梯度值 - 更新参数（梯度下降）

定义神经网络的结构

主要任务是描述网络各个层的节点个数

1
2
3
4
5
def layer_sizes(X, Y):
    n_x = X.shape[0]  # 输入层单元数量
    n_h = 4  # 隐藏层单元数量，在这个模型中，我们设置成4即可
    n_y = Y.shape[0]  # 输出层单元数量
    return (n_x, n_h, n_y)

随机初始化参数

参数W的随机初始化是很重要的，如果W和b都初始化成0，那么这一层的所有单元的输出值都一样，导致反向传播时，所有的单元的参数都做出完全相同的调整，这样多个单元的效果和只有一个单元的效果是相同的。那么多层神经网络就没有任何意义。为了避免这样的情况发生，我们会把参数W初始化成非零。

另外，随机初始化W之后，我们还会乘上一个较小的常数，比如 0.01 ，这样是为了保证输出值 Z 数值都不会太大。为什么这么做？设想我们用的激活函数是 sigmoid 或者 tanh ，那么，太大的 Z 会导致最终 A 会落在函数图像中比较平坦的区域内，这样的地方梯度都接近于0，会降低梯度下降的速度，因此我们会将权重初始化为较小的随机值。

1
2
3
4
5
6
7
8
9
10
11
def initialize_parameters(n_x, n_h, n_y):
  #随机初始化
    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    return parameters

循环迭代

实现正向传播

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def forward_propagation(X, parameters):
    # 从parameters中取出参数
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    # 执行正向传播操作
    Z1 = np.dot(W1, X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2, A1) + b2
    A2 = sigmoid(Z2)
    #如果不相等，直接报错
    assert (A2.shape == (1, X.shape[1]))
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    return A2, cache

计算成本函数J

1
2
3
4
5
6
7
8
9
10
11
def compute_cost(A2, Y, parameters):
    m = Y.shape[1]  # 样本个数
    # 下一行的结果是 (1, m)的矩阵
    logprobs = np.multiply(Y, np.log(A2)) + np.multiply(1 - Y, np.log(1 - A2))
    # 将 (1, m)的矩阵求和后取平均值
    cost = - 1 / m * np.sum(logprobs)
    # np.squeeze()函数对矩阵进行压缩维度，删除单维度条目，即把shape中为1的维度去掉
    # 例如： np.squeeze([[ 1.23 ]]) 可以将维度压缩，最终变成 1.23
    # 目的是确保 cost 是一个浮点数
    cost = np.squeeze(cost)
    return cost

利用正向传播函数返回的cache，我们可以实现反向传播了。

实现反向传播

说明：

我们使用的 g^[1] () 是 tanh ，并且 A1 = g^[1] ( Z^[1] ) ,那么求导变形后可以得到 g‘ ^[1] ( Z^[1] ) = 1-( A^[1] )^2 用python表示为： 1 - np.power(A1, 2)

我们使用的 g^[2] () 是 sigmoid ，并且 A2 = g^[2] ( Z^[2] ) ,那么求导变形后可以得到 g‘ ^[2] ( Z^[2] ) =A^2 - Y

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def backward_propagation(parameters, cache, X, Y):
    # 获取样本的数量
    m = X.shape[1]
    # 从 parameters 和 cache 中取得参数
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    A1 = cache["A1"]
    A2 = cache["A2"]
    # 计算梯度 dW1, db1, dW2, db2.
    dZ2 = A2 - Y
    dW2 = 1 / m * np.dot(dZ2, A1.T)
    db2 = 1 / m * np.sum(dZ2, axis=1, keepdims=True)
    dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
    dW1 = 1 / m * np.dot(dZ1, X.T)
    db1 = 1 / m * np.sum(dZ1, axis=1, keepdims=True)
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    return grads

说明

1、计算db^[1]和db^[2]时的程序代码的sum函数的第二个参数 axis=1 表示水平相加求和。

2、 keepdims=True是为了保持矩阵的shape属性值是我们熟悉的()中有两个数字的形式，例如(1, m)，(4, m)等，如果不加上可能得到的是奇怪的(1, )，(4, )这样的形式。

更新参数

利用上面反向传播的代码段获得的梯度去更新 (W1, b1, W2, b2)：

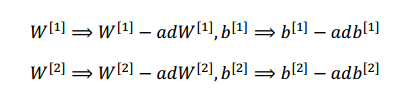
式子中 α 是学习率，较小的学习率的值会降低梯度下降的速度，但是可以保证成本函数 J 可以在最小值附近收敛，而较大的学习率让梯度下降速度较快，但是可能会因为下降的步子太大而越过最低点，最终无法在最低点附近出收敛。

本篇博客选择1.2作为学习率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def update_parameters(parameters, grads, learning_rate=1.2):
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]

    # 更新参数
    W1 -= learning_rate * dW1
    b1 -= learning_rate * db1
    W2 -= learning_rate * dW2
    b2 -= learning_rate * db2
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    return parameters

构建完整的神经网络模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
    # 输入层单元数
    n_x = layer_sizes(X, Y)[0] 
    # 输出层单元数
    n_y = layer_sizes(X, Y)[2] 
    
    # 随机初始化参数
    parameters = initialize_parameters(n_x, n_h, n_y) 
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    # 10000次梯度下降的迭代
    for i in range(0, num_iterations):
        # 正向传播，得到Z1、A1、Z2、A2
        A2, cache = forward_propagation(X, parameters)
        
        # 计算成本函数的值
        cost = compute_cost(A2, Y, parameters)
 
        # 反向传播，得到各个参数的梯度值
        grads = backward_propagation(parameters, cache, X, Y)
 
        # 更新参数
        parameters = update_parameters(parameters, grads, learning_rate = 1.2)
        
        # 每迭代1000下就输出一次cost值
        if print_cost and i % 1000 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))

    # 返回最终训练好的参数
    return parameters

对样本进行预测

我们约定 预测值大于0.5的之后取1，否则取0：

对一个矩阵M而言，如果你希望它的每个元素 如果大于某个阈值 threshold 就用1表示，小于这个阈值就用 0 表示，那么，在python中可以这么实现：M_new = (M > threshold)

1
2
3
4
def predict(parameters, X):
    A2, cache = forward_propagation(X, parameters)
    predictions = (A2 > 0.5)
    return predictions

利用模型预测

1
2
3
4
5
6
7
8
9
# 利用含有4个神经元的单隐藏层的神经网络构建分类模型
parameters = nn_model(X, Y, n_h=4, num_iterations=10000, print_cost=True)
# 可视化分类结果
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
plt.show()
# 输出准确率
predictions = predict(parameters, X)
print('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')

尝试换一下隐藏层的单元个数

1
2
3
4
5
6
7
8
9
10
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 10, 20]
for i, n_h in enumerate(hidden_layer_sizes):
    plt.subplot(5, 2, i+1)
    plt.title('Hidden Layer of size %d' % n_h)
    parameters = nn_model(X, Y, n_h, num_iterations = 5000)
    plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
    predictions = predict(parameters, X)
    accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)
    print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))

换数据集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Datasets
noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()
datasets = {"noisy_circles": noisy_circles,
            "noisy_moons": noisy_moons,
            "blobs": blobs,
            "gaussian_quantiles": gaussian_quantiles}
# 在这里选择你要选用的数据集
dataset = "noisy_circles"
X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])
# make blobs binary
if dataset == "blobs":
    Y = Y%2
# 可视化数据
plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral);
plt.show()
# 测试代码如下：
parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)
# 画出边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
plt.show()
----本文结束，感谢您的阅读。如有错，请指正。----
大哥大嫂过年好！支持我一下呗
0%