神经网络概览
在逻辑回归中,我们的模型大概是这样的,得到的a即是预测结果y帽。
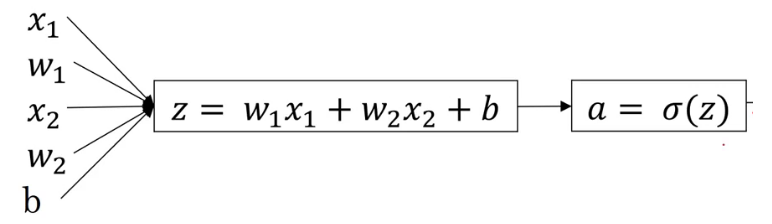
如果把上面的图片抽象化,可以得到以下模型:

再进一步简化得到:
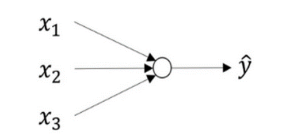
上图里,小圆圈是sigmoid单元,它要完成的工作就是先计算 z 然后计算 a 最终作为 y帽 输出。
进而,我们看看下图,这是较为简单的神经网络的样子,它无非就是将多个 sigmoid 单元组合在一起,形成了更复杂的结构。图中每个单元都需要接收数据的输入,并完成数据的输出,其每个单元的计算过程与 logistic回归 的正向传播类似。可以看到,图片里给神经网络分了层次,最左边的是输入层,也就是第0层;中间的是隐藏层,也就是第一层;最右边的是输出层,是第二层。通常,我们不将输入层看做神经网络的一层,因而下图是一个2层的神经网络。 另外要清楚的是,本图中隐藏层只有一个,但实际上,隐藏层可以有多个。由于对用户而言,隐藏层计算得到的数据用户不可预见,也没有太大必要知道,所以称之为隐藏层。也正是因为如此,神经网络的解释器很差。
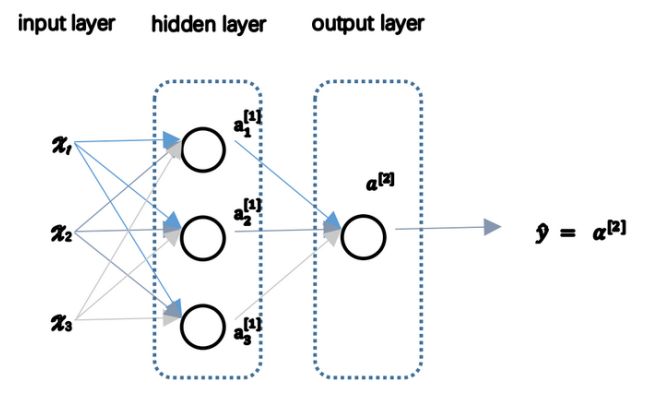
再进一步认识下这张图片里的标记,隐藏层的每个单元都需要接收输入层的数据,并且各个单元都需要计算 z , 并经过 sigmoid 函数得到各自的 a ,为了便于区分不同层的不同单元的 a,我们做如下约定:
a 的右上角有个角标[i],表示这是第i层的单元;a 的右下角有个角标 j 用于区分这是该层自上向下的第 j 个单元。例如我们用 a^[1]_3 表示这是第一层的第三个单元。输入层的 x1, x2, … xn 可以看做是 a^[0]_1, a^[0]_2 … a^[0]_n.
前一层a[ i ] 的输出,便是后一层 a[ i+1 ] 的所有单元输入。除了输入层外的其它层,也就是隐藏层和输出层的单元都有各自的参数 w 和 b 用于计算 z ,同样是用w^[i]_j, b^[i]_j, z^[i]_j 来区分他们;得到 z^[i]_j 后用sigmoid函数计算 a^[i]_j ,再将本层n个单元计算得到的n个 a 作为下一层的输入,最终在输出层得到预测值 y帽。其计算过程大致如下:

计算一个样本的神经网络输出
下图是输入单个样本(该样本含有特征x1, x2, x3)的神经网络图,隐藏层有4个单元:

根据上面的说明,要计算该神经网络的输出,我们首先要计算隐藏层4个单元的输出
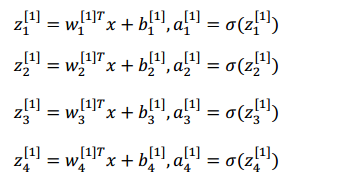
第一步就是计算第一层各个单元的 z^[1]_j ,第二步是计算出各个单元的 a^[i]_j,不难想到可以用向量化计算来化简上述操作,我们将所有 w^[1]_j 的转置纵向叠加得到下图的内容,我们将这个大的矩阵记为W^[1],得出下图:
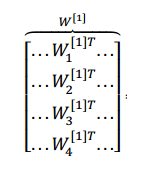
由于输入的 x 是三维的列向量,所以每个分量x1, x2, x3 都需要一个 w1, w2, w3 对应,因此 w^[1]_j 的转置是一个(1, 3) 的矩阵,又因为隐藏层有4个单元,即 j 的取值为1, 2, 3, 4,故 W^[1] 是 (4, 3) 的矩阵。
同理,第二层,也就是输出层的 W^[2] 由于有4个输入的特征,1个单元,所以 W^[2] 是 (1, 4)的矩阵。
对于只有一个样本的情况,我们不难得到如下式子:

z^[1] 是个 (4, 1) 的矩阵。可以再进一步通过 sigmoid 函数得到

至此,第一层神经网络得任务已完成
第二层也就是输出层的工作,无非就是把第一层的 a^[1] 作为输入,继续用 W^[2] 与 a^[1] 相乘 再加上 b^[2] 得到 z^[2],再通过 sigmoid 函数得到 a^[2] 也就是最终的预测结果 y帽。
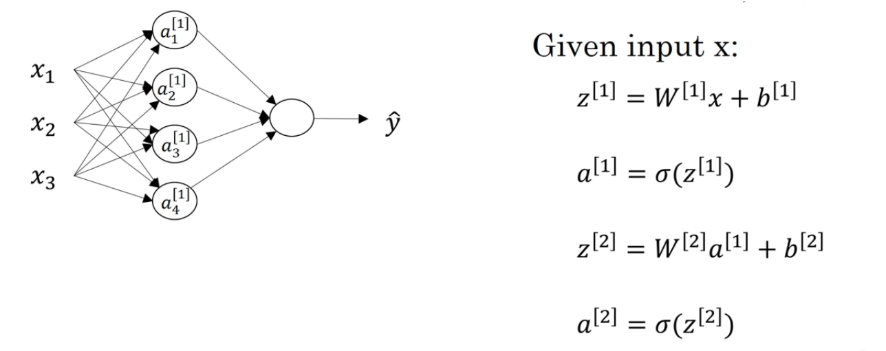
至此,我们就完成了一个样本的输出。接下来看看如何用矩阵实现多样本的正向输出。
计算多样本的输出
假设我们有m个样本,每个样本有3个特征,并且隐藏层也是4个单元。
那么,通常我们需要使用一个 for 循环将 从 1 遍历至 m 完成以下操作:

角标 ^(i) 表示第 i 个样本。我们可以构造这样一个矩阵 x:

它将所有样本的特征,按列叠加在一起,构成 (3, m) 的矩阵。
如果我们替换上面计算 z^[1] 的过程中使用的 单个样本 x^(1) 为(3, m) 的矩阵 x (也就是下图的绿色框):

就可以得到下面的式子(为了方便表达,下面的公式中假设 b 等于0):
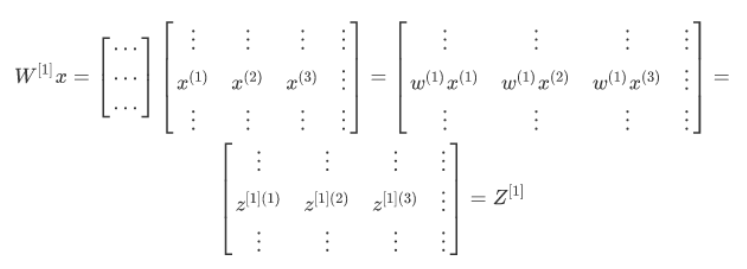
到这里,我们求出了 Z^[1] ,并且由于 Z^[1] 是(4, 3)的矩阵W^[1]乘以(3, m)的矩阵x 再加上b,所以它是 (4, m) 的矩阵。再经过 sigmoid 函数即可得到同样是 (4, m) 的矩阵 A^[1],到此隐藏层的工作完成了。
输出数据
矩阵 A^[1],作为下一层(也就是输出层)的输入参数,经过类似的计算也可以得到 Z^[2] = W^[2] × A^[1] + b^[2],上面我们分析到 W^[2] 是 (1, 4)的矩阵,所以得到的Z^[2]是 (1, m) 的矩阵,同样经过sigmoid函数处理得到的 A^[2] 也是 (1, m) 的矩阵,A^[2]的每个元素,代表一个样本输出的预测值。

