符号约定
首先看下图:

我们假设n[l] 表示第 l 层的神经元的数量,那么这个单隐层的神经网络的输入层、隐含层和输出层的维度分别是:n[0]= n_x =3、n[1]=4、n[2]=1。
那么根据浅层神经网络的正向传播)的分析,如果一次性输入带有 m 个样本的矩阵 X 我们可以得到:
W^[1] = (4, 3), Z^[1] = (4, m), A^[1] = (4, m)
W^[2] = (1, 4), Z^[2] = (1, m), A^[2] = (1, m)
可以总结出如下规律,对第 l 层的单元而言:
W^[l] = (n^[l], n^[l-1]),
Z^[l] = (n^[l], m),
A^[l] = (n^[l], m).
另外,还有一个规律:
对任意层而言:
dW 的维度和 W 的维度相同
dZ 的维度和 Z 的维度相同
dA 的维度和 A 的维度相同
注意:以上出现的符号都是将m个样本向量化后的表达。
单个样本的梯度计算
讲反向传播前,我们先回顾一下单个样本的正向传播的过程:

其中计算z^[1]时用到的 x 可以看做是 a^[0],σ( ) 是激活函数中一种,一般情况下,我们更习惯用用 g( ) 来表示激活函数。于是将上述式子一般化可以得到第 l 层的公式为:
z^[l] = W^[l]a^[l-1] + b^[l] ————- ①
a^[l] = g^[l] ( z^[l] ) —————————- ②
由于我们输入的样本只有一个,所以各个向量的维度如下:
W^[l] = (n^[l], n^[l-1]),
z^[l] = (n^[l], 1),
a^[1] = (n^[l], 1).
我们现在根据式子 ① 和 ② 来讨论反向传播的过程。
因为正向传播的时候我们依次计算了z^[1], a^[1], z^[2], a^[2]最终得到了损失函数L。所以反向传播的时候,我们要从L向前计算梯度。
第一步计算dz^[2]和da^[2]进而算出 dW^[2] 和 db^[2]:
da^[2]=dL/da^[2]= -y/a^[2]+(1-y)/(1-a^[2])
dz^[2]= dL/dz^[2] = dL/da^[2]*da^[2]/dz^[2]=-y(1-a^[2])+(1-y)a^[2] = a^[2] - y
说明1:
dz^[2] 的维度和z^[2]相同,da^[2] 的维度和a^[2]相同,为(1, 1)
g’( z^[2] ) 的维度与 z^[2]维度相同,为(1, 1)
在第二层中,a^[2] 与 z^[2]的维度也相同,为(1, 1)
实际上,dz^[2] 应该等于da^[2] 与 g’( z^[2] ) 的内积的结果,理由我们我们先向下看
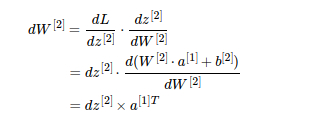
说明2 :
上图中我们可以得到 dW^[2] = dz^[2]乘上 a^[1] 的转置,这里是因为 :
dW^[2] 和 W^[2] 的形状是一样的(n^[2], n^[1])也就是(1, 4),
dz^[2] 和 z^[2] 的形状是一样的(n^[2], 1)也就是(1, 1),
a^[1] 的形状是 (n^[1], 1) 也就是(4, 1),可以得到 a^[1] 的转置 a^( [1]T ) 的形状是 (1, 4),
这样 dz^[2] 和 a^[1] 的转置 的乘积的形状才能是 dW^[2] 的形状 (1, 4);
因此 dW^[2] = dz^[2]乘上 a^[1] 的转置。
这里给我们的启发是:向前求导的时候注意矩阵的维度变化,通过分析矩阵的维度来判断矩阵是否需要进行转置操作。
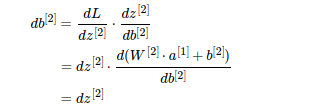
第二步计算 da^[1] 和 dz^[1]进而算出 dW^[1] 和 db^[1]

检查矩阵形状是否匹配:(4,1)* (1,1),匹配
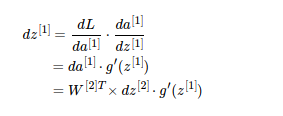
说明3:
dz^[1] 的维度和z^[1]相同,da^[1] 的维度和a^[1]相同,均为(4, 1)
W^[2]T 的维度是 (4, 1),dz^[2] 的维度是 (1, 1) ,二者的乘积与da^[1] 维度相同。
g’( z^[1] ) 的维度与 z^[1]维度相同,也与da^[1] 维度相同,为(4, 1)。
所以想得到维度为 (4, 1) 的dz^[1] ,da^[1] 与 g’( z^[1] ) 直接的关系为内积
这里给我们的启发是:向前求导的时候注意矩阵的维度变化,通过分析矩阵的维度来判断矩阵是否需要进行内积操作。这里就解释了说明(1)留下的问题。
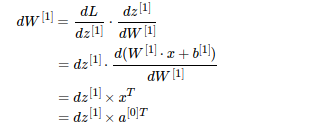
检查维度:(4,3)=(4,1)*(1,3),正确

公式:
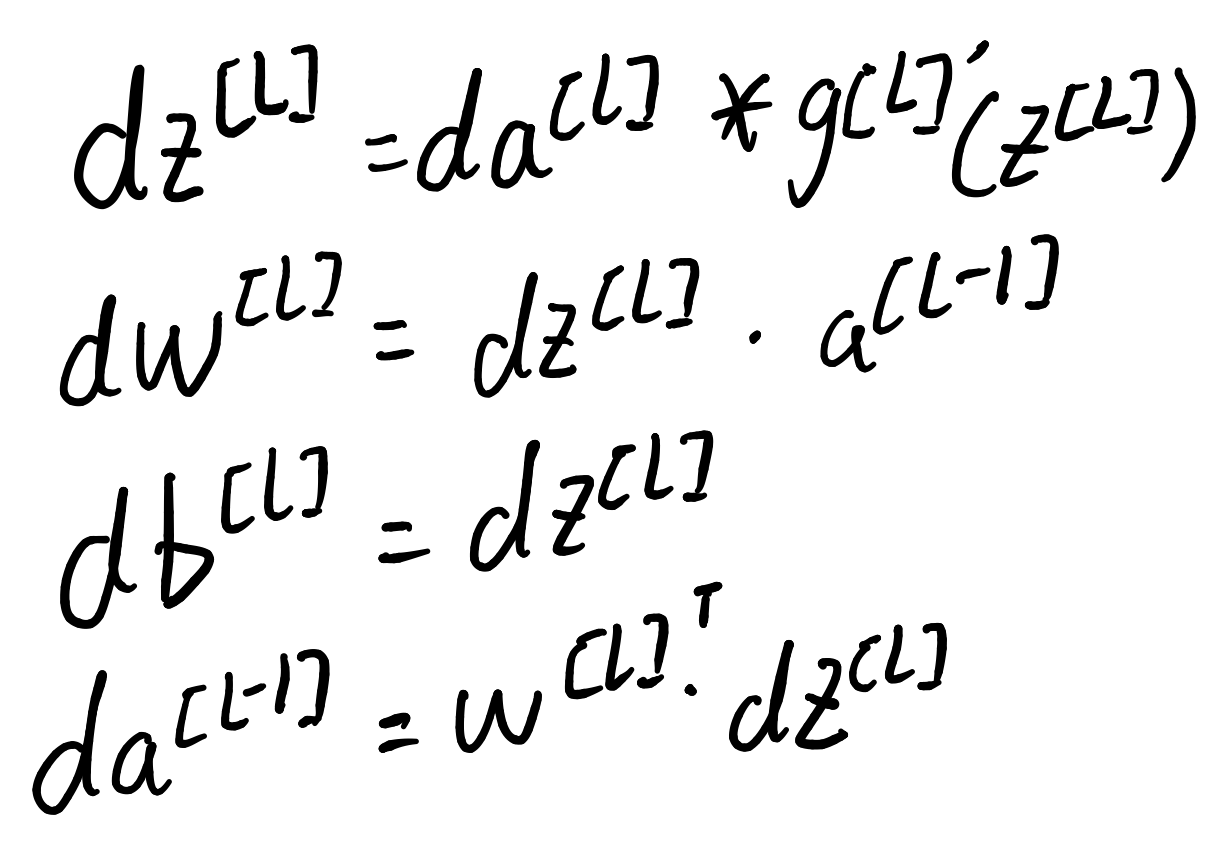
多个样本的梯度运算
用m个样本作为输入,并进行向量化后正向传播的公式:
Z^[1] = W^[1]X + b^[1]
A^[1] = g^[1] ( Z^[1] )
Z^[2] = W^[2]A^[1] + b^[2]
A^[2] = g^[2] ( Z^[2] )
由于引入了m个样本,我们也要有个成本函数来衡量整体的表现情况,我们的目的是让J达到最小值
下图中左边列举了我们上面所推导的各种式子,其中图中所用的激活函数 g^[2] () 为sigmoid函数,因而dz^[2] = a^[2] - y。这些左边的式子都是针对单个样本而言的,而右边则是将m个样本作为输入并向量化后的公式的表达形式。

上图的说明:
1、由于成本函数 J 是所有的 损失函数 L 的值求和后的平均值, 那么 J 对 W^[1], b^[1], W^[2], b^[2] 的导数 等价于 各个 L 对 W^[1], b^[1], W^[2], b^[2] 的导数求和后的平均值。所以dW^[1], db^[1], dW^[2], db^[2]的式子中需要乘上 1 / m。
2、计算db^[1]和db^[2]时的程序代码的sum函数的第二个参数 axis=1 表示水平相加求和。
3、keepdims=True是为了保持矩阵的shape属性值是我们熟悉的()中有两个数字的形式,例如(1, m),(4, m)等,如果不加上可能得到的是奇怪的(1, ),(4, )这样的形式。
更新参数
最后,不要忘了要更新参数(式子中的α是学习率)
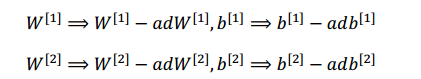
总的来说,反向传播就是训练模型参数,在所有参数上使用梯度下降,使模型在训练数据上的损失函数变小

