使用SVC时的其他考虑
SVC处理多分类问题
之前的所有的SVM的(1)-(3)内容,全部是基于二分类的情况来说明的。因为支持向量机是天生二分类的模型。但是,它也可以做多分类。但是SVC在多分类情况的推广是很难的。因为要研究透彻多分类状况下的SVC,就必须研究透彻多分类时所需要的决策边界个数,每个决策边界所需要的支持向量个数,以及这些支持向量如何组合起来计算拉格朗日乘数。本小节只说一小部分。支持向量机是天在生二分类的模型,所以支持向量机在处理多分类问题的时候,是把多分类问题转换成了二分类问题来解决。这种转换有两种模式,一种叫做“一对一”模式(one vs one),一种叫做“一对多”模式(one vs rest)。
在ovo模式下(一对一模式)上,标签中的所有类别都会被两两组合,每两个类别建立一个SVC模型,每个模型生成一个决策边界,分别进行二分类,这种模式下,对于n_class个标签类别的数据来说,SVC会生成总共$C^2_{n_class}$个模型,即会生成总共$C^2_{n_class}$个超平面,其中:

ovo模式下,二维空间的三分类状况:
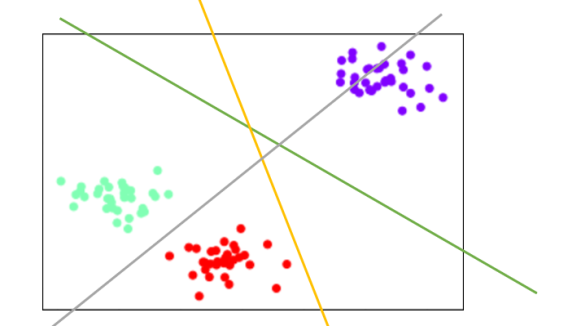
首先让提出紫色点和红色点作为一组,然后求解出两个类之间的SVC和绿色决策边界。然后让绿色点和红色点作为一组,求解出两个类之间的SVC和灰色边界。最后让绿色和紫色组成一组,组成两个类之间的SVC和黄色边界。然后基于三个边界,分别对三个类别进行分类。
ovr模式下,标签中所有的类别会分别于其他类别进行组合,建立n_class个模型,每个模型生成一个决策边界。分别进行二分类。ovr模式下,则会生成以下的决策边界:
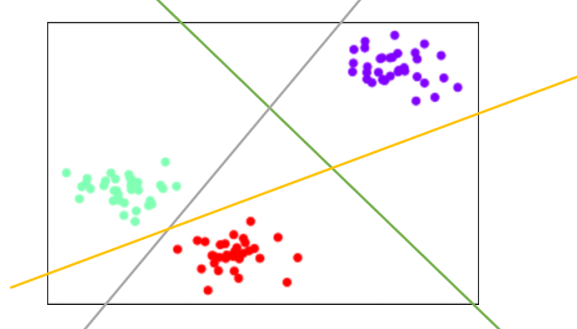
紫色类 vs 剩下的类,生成绿色的决策边界。红色类 vs 剩下的类,生成黄色的决策边界。绿色类 vs 剩下的类,生成灰色的决策边界,当类别更多的时候,如此类推下去,我们永远需要n_class个模型。
当类别更多的时候,无论是ovr还是ovo模式需要的决策边界都会越来越多,模型也会越来越复杂,不过ovo模式下的模型计算会更加复杂,因为ovo模式中的决策边界数量增加更快,但相对的,ovo模型也会更加精确。ovr模型计算更快,但是效果往往不是很好。在硬件可以支持的情况下,还是建议选择ovo模式。
模型和超平面的数量变化了,SVC的很多计算、接口、属性都会发生变化,而参数decision_function_shape决定我们究竟使用哪一种分类模式。
decision_function_shape
可输入“ovo”,”ovr”,默认”ovr”,对所有分类器,选择使用ovo或者ovr模式。
选择ovr模式,则返回的decision_function结构为(n_samples,n_class)。但是当二分类时,尽管选用ovr模式,却会返回
(n_samples,)的结构。
选择ovo模式,则使用libsvm中原始的,结构为(n_samples,n_class(n_class-1)/2)的decision_function接口。在ovo模式并且核函数为线性核的情况下,属性coef_和intercepe_会分别返回(n_class\(n_class-1)/2,n_features) 和(n_class*(n_class-1)/2,)的结构,每行对应一个生成的二元分类器。ovo模式只在多分类的状况下使用。
SVC的其它参数、属性和接口的列表在SVM解读(2)/#more](https://brickexperts.github.io/2019/09/15/SVM解读(2)/#more)
线性支持向量机类LinearSVC

线性支持向量机其实与SVC类中选择”linear”作为核函数的功能类似,但是其背后的实现库是liblinear而不是libsvm,这使得在线性数据上,linearSVC的运行速度比SVC中的“linear”核函数要快,不过两者的运行结果相似。在现实中,许多数据都是线性的,因此我们可以依赖计算得更快得LinearSVC类。除此之外,线性支持向量可以很容易地推广到大样本上,还可以支持稀疏矩阵,多分类中也支持ovr方案。

和SVC一样,LinearSVC也有C这个惩罚参数,但LinearSVC在C变大时对C不太敏感,并且在某个阈值之后就不能再改善结果了。

