SVM解读(3)

发表于 更新于 分类于 ，

参数C的理解进阶

在SVM(2)说到有一些数据，可能是线性可分，但在线性可分状况下训练准确率不能达到100%，即无法让训练误差为0，这样的数据被我们称为“存在软间隔的数据”。此时此刻，我们需要让我们决策边界能够忍受一小部分训练误差，我们就不能单纯地寻求最大边际了。 因为对于软间隔地数据来说，边际越大被分错的样本也就会越多，因此我们需要找出一个”最大边际“与”被分错的样本数量“之间的平衡。因此，我们引入松弛系数ζ和松弛系数的系数C作为一个惩罚项，来惩罚我们对最大边际的追求。

那我们的参数C如何影响我们的决策边界呢？在硬间隔的时候，我们的决策边界完全由两个支持向量和最小化损失函数（最大化边际）来决定，而我们的支持向量是两个标签类别不一致的点，即分别是正样本和负样本。然而在软间隔情况下我们的边际依然由支持向量决定，但此时此刻的支持向量可能就不再是来自两种标签类别的点了，而是分布在决策边界两边的，同类别的点。回忆一下我们的图像：

此时我们的虚线超平面ω*x+b=1-ζi是由混杂在红色点中间的紫色点来决定的，所以此时此刻，这个蓝色点就是我们的支持向量了。所以软间隔让决定两条虚线超平面的支持向量可能是来自于同一个类别的样本点，而硬间隔的时候两条虚线超平面必须是由来自两个不同类别的支持向量决定的。而C值会决定我们究竟是依赖红色点作为支持向量（只追求最大边界），还是我们要依赖软间隔中，混杂在红色点中的紫色点来作为支持向量（追求最大边界和判断正确的平衡）。如果C值设定比较大，那SVC可能会选择边际较小的，能够更好地分类所有训练点的决策边界，不过模型的训练时间也会更长。如果C的设定值较小，那SVC会尽量最大化边界，尽量将掉落在决策边界另一方的样本点预测正确，决策功能会更简单，但代价是训练的准确度，因为此时会有更多红色的点被分类错误。换句话说，C在SVM中的影响就像正则化参数对逻辑回归的影响。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import svm
from sklearn.datasets import make_circles, make_moons, make_blobs,make_classification
n_samples = 100
datasets = [
make_moons(n_samples=n_samples, noise=0.2, random_state=0),
make_circles(n_samples=n_samples, noise=0.2, factor=0.5, random_state=1),
make_blobs(n_samples=n_samples, centers=2, random_state=5),
make_classification(n_samples=n_samples,n_features =
2,n_informative=2,n_redundant=0, random_state=5)
]
Kernel = ["linear"]
#四个数据集分别是什么样子呢？
for X,Y in datasets:
    plt.figure(figsize=(5,4))
    plt.scatter(X[:,0],X[:,1],c=Y,s=50,cmap="rainbow")
nrows=len(datasets)
ncols=len(Kernel) + 1
fig, axes = plt.subplots(nrows, ncols,figsize=(10,16))
    #第一层循环：在不同的数据集中循环
for ds_cnt, (X,Y) in enumerate(datasets):
    ax = axes[ds_cnt, 0]
    if ds_cnt == 0:
        ax.set_title("Input data")
    ax.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.Paired,edgecolors='k')
    ax.set_xticks(())
    ax.set_yticks(())
    for est_idx, kernel in enumerate(Kernel):
        ax = axes[ds_cnt, est_idx + 1]
        clf = svm.SVC(kernel=kernel, gamma=2).fit(X, Y)
        score = clf.score(X, Y)
        ax.scatter(X[:, 0], X[:, 1], c=Y
                   , zorder=10
                   , cmap=plt.cm.Paired, edgecolors='k')
        ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
                   facecolors='none', zorder=10, edgecolors='white')
        x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
        y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
        XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
        Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()]).reshape(XX.shape)
        ax.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.Paired)
        ax.contour(XX, YY, Z, colors=['k', 'k', 'k'], linestyles=['--', '-', '--'],
                   levels=[-1, 0, 1])
        ax.set_xticks(())
        ax.set_yticks(())
        if ds_cnt == 0:
            ax.set_title(kernel)
        ax.text(0.95, 0.06, ('%.2f' % score).lstrip('0')
                , size=15
                , bbox=dict(boxstyle='round', alpha=0.8, facecolor='white')
                # 为分数添加一个白色的格子作为底色
                , transform=ax.transAxes  # 确定文字所对应的坐标轴，就是ax子图的坐标轴本身
                , horizontalalignment='right'  # 位于坐标轴的什么方向
                )
plt.tight_layout()
plt.show()

白色圈圈出的就是我们的支持向量，大家可以看到，所有在两条虚线超平面之间的点，和虚线超平面外，但属于另一个类别的点，都被我们认为是支持向量。并不是因为这些点都在我们的超平面上，而是因为我们的超平面由所有的这些点来决定，我们可以通过调节C来移动我们的超平面，让超平面过任何一个白色圈圈出的点。参数C就是这样影响了我们的决策，可以说是彻底改变了SVM的决策过程。

样本不均衡问题

分类问题永远逃不过的痛点是样本不均衡问题。样本不均衡是指在一组数据集中，标签的一类天生占有很大的比例，但我们有着捕捉出某种特定的分类的需求的状况。

分类问题天生会倾向于多数的类，让多数类更容易被判断准确，少数类被牺牲掉。因此对于模型而言，样本量越大的标签可以学习的信息越多，算法就会更加依赖于从多数类中学到的信息来进行判断。如果我们希望捕获少数类，模型就会失败。其次，模型评估指标会失去意义。

class_weight

可输入字典或者”balanced”，可不填，默认None 对SVC，将类i的参数C设置为class_weight [i] C。如果没有给出具体的class_weight，则所有类都被假设为占有相同的权重1，模型会根据数据原本的状况去训练。如果希望改善样本不均衡状况，请输入形如{“标签的值1”：权重1，”标签的值2”：权重2}的字典，则参数C将会自动被设为：标签的值1的C：权重1 C，标签的值2的C：权重2C或者，可以使用“balanced”模式，这个模式使用y的值自动调整与输入数据中的类频率成反比的权重为n_samples/(n_classes np.bincount(y)) 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs
class_1 = 500 #类别1有500个样本
class_2 = 50 #类别2只有50个
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [1.5, 0.5] #设定两个类别的方差，通常来说，样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False)
#看看数据集长什么样
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=10)
#其中红色点是少数类，紫色点是多数类
clf = svm.SVC(kernel='linear', C=1.0)
clf.fit(X, y)
#设定class_weight
wclf = svm.SVC(kernel='linear', class_weight={1: 10})
wclf.fit(X, y)
#给两个模型分别打分看看，这个分数是accuracy准确度
print("没设定class_weight：",clf.score(X,y))
print("设定class_weight：",wclf.score(X,y))
plt.figure(figsize=(6,5))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=10)
ax = plt.gca() #获取当前的子图，如果不存在，则创建新的子图
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
#第二步：找出我们的样本点到决策边界的距离
Z_clf = clf.decision_function(xy).reshape(XX.shape)
a = ax.contour(XX, YY, Z_clf, colors='black', levels=[0], alpha=0.5, linestyles=['-'])
Z_wclf = wclf.decision_function(xy).reshape(XX.shape)
b = ax.contour(XX, YY, Z_wclf, colors='red', levels=[0], alpha=0.5, linestyles=['-'])
#第三步：画图例 a.collections调用这个等高线对象中画的所有线，返回一个惰性对象
plt.legend([a.collections[0], b.collections[0]], ["non weighted", "weighted"],
loc="upper right")
plt.show()

从图像上可以看出，灰色是我们做样本平衡之前的决策边界。灰色线上方的点被分为一类，下方的点被分为另一类。可以看到，大约有一半少数类（红色）被分错，多数类（紫色点）几乎都被分类正确了。红色是我们做样本平衡之后的决策边界，同样是红色线上方一类，红色线下方一类。可以看到，做了样本平衡后，少数类几乎全部都被分类正确了，但是多数类有许多被分错了。

从准确率的角度来看，不做样本平衡的时候准确率反而更高，做了样本平衡准确率反而变低了，这是因为做了样本平衡后，为了要更有效地捕捉出少数类，模型误伤了许多多数类样本，而多数类被分错的样本数量 > 少数类被分类正确的样本数量，使得模型整体的精确性下降。现在，如果我们的目的是模型整体的准确率，那我们就要拒绝样本平衡，使用class_weight被设置之前的模型。而在现实情况中，我们往往都在捕捉少数类。因为有些情况是宁愿误伤，也要尽量的捕捉少数类。

SVC的模型评估指标

上面说了，我们往往都在捕捉少数类的。但是单纯地追求捕捉出少数类，就会成本太高，而不顾及少数类，又会无法达成模型的效果。所以在现实中，我们往往在寻找捕获少数类的能力和将多数类判错后需要付出的成本的平衡。如果一个模型在能够尽量捕获少数类的情况下，还能够尽量对多数类判断正确，则这个模型就非常优秀了。为了评估这样的能力，我们将引入新的模型评估指标：混淆矩阵和ROC曲线来帮助我们

混淆矩阵(Confusion Matrix)

精确率和召回率

精确度Precision，又叫查准率，表示所有被我们预测为是少数类的样本中，真正的少数类所占的比例

召回率Recall，又被称为敏感度(sensitivity)，真正率，查全率，表示所有真实为1的样本中，被我们预测正确的样
本所占的比例。

如果我们希望不计一切代价，找出少数类，那我们就会追求高召回率，相反如果我们的目标不是尽量捕获少数类，那我们就不需要在意召回率。 注意召回率和精确度的分子是相同的，只是分母不同。而召回率和精确度是此消彼长的，两者之间的平衡代表了捕捉少数类的需求和尽量不要误伤多数类的需求的平衡。究竟要偏向于哪一方，取决于我们的业务需求：
究竟是误伤多数类的成本更高，还是无法捕捉少数类的代价更高。

为了同时兼顾精确度和召回率，我们创造了两者的调和平均数作为考量两者平衡的综合性指标，称之为F1measure。两个数之间的调和平均倾向于靠近两个数中比较小的那一个数，因此我们追求尽量高的F1 measure，能够保证我们的精确度和召回率都比较高。F1 measure在[0,1]之间分布，越接近1越好：

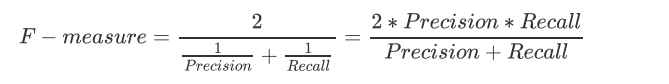
假负率、特异度(真负率)、假正率

从Recall延申出来的另一个评估指标叫做假负率（False Negative Rate），它等于 1 - Recall，用于衡量所有真实为1的样本中，被我们错误判断为0的，通常用得不多。

特异度(Specificity)，也叫做真负率。表示所有真实为0的样本中，被正确预测为0的样本所占的比例。在支持向量机中，可以形象地表示为，决策边界下方的点占所有蓝色点的比例。特异度衡量了一个模型将多数类判断正确的能力，而1 - specificity就是一个模型将多数类判断错误的能力，叫做假正率。

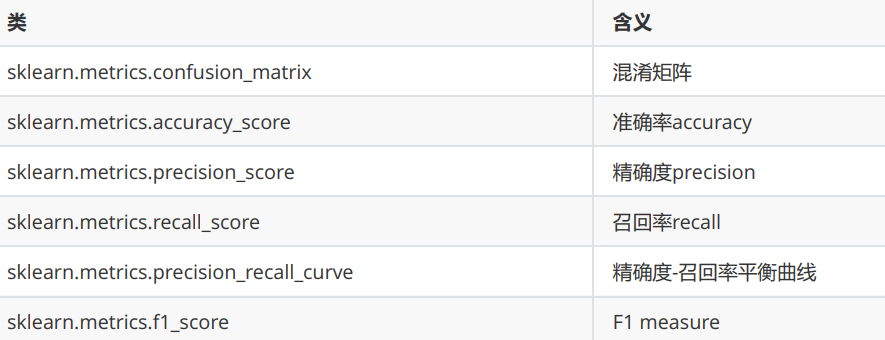
sklearn当中提供了大量的类来帮助我们了解和使用混淆矩阵：

ROC曲线

ROC曲线，全称The Receiver Operating Characteristic Curve，译为受试者操作特性曲线。这是一条以不同阈值下的假正率FPR为横坐标，不同阈值下的召回率Recall为纵坐标的曲线。让我们先从概率和阈值开始看起。

阈值(threshold)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs
class_1 = 500 #类别1有500个样本
class_2 = 50 #类别2只有50个
centers = [[0.0, 0.0], [1.0, 1.0]] #设定两个类别的中心
clusters_std = [0.5, 1] #设定两个类别的方差，通常来说，样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False)
#看看数据集长什么样
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=30)
plt.show()
from sklearn.linear_model import LogisticRegression as LogiR
clf_lo=LogiR().fit(X,y)
prob=clf_lo.predict_proba(X)
import pandas as pd
prob=pd.DataFrame(prob)
prob.columns=["0","1"]
for i in range(prob.shape[0]):
    #将0.5设立为阈值
    if prob.loc[i,"1"] > 0.5:
    #创建了一个新的列名为pred的列
        prob.loc[i,"pred"] = 1
    else:
        prob.loc[i,"pred"] = 0
#创建了名为y_true的列，且将y赋值为该列
prob["y_true"] = y
#通过“1”列拍序，ascending表示正序or逆序
prob = prob.sort_values(by="1",ascending=False)
from sklearn.metrics import confusion_matrix as CM, precision_score as P, recall_score as R
from sklearn.metrics import accuracy_score as A
print("混淆矩阵：",CM(prob.loc[:,"y_true"],prob.loc[:,"pred"],labels=[1,0]))
print("精确度：",P(prob.loc[:,"y_true"],prob.loc[:,"pred"],labels=[1,0]))
print("召回率：",R(prob.loc[:,"y_true"],prob.loc[:,"pred"],labels=[1,0]))
print("准确率：",A(prob.loc[:,"y_true"],prob.loc[:,"pred"]))

我们可以设置不同阈值来实验模型的结果，在不同阈值下，我们的模型评估指标会发生变化。我们正利用这一点来观察Recall和FPR之间如何互相影响。但是注意，并不是升高阈值，就一定能够增加或者减少Recall，一切要根据数据的实际分布来进行判断。

概率(probability)

我们在画等高线，也就是决策边界的时候曾经使用SVC的接口decision_function，它返回我们输入的特征矩阵中每个样本到划分数据集的超平面的距离。我们在SVM中利用超平面来判断我们的样本，本质上来说，当两个点的距离是相同的符号的时候，越远离超平面的样本点归属于某个标签类的概率就很大。比如说，一个距离超平面0.1的点，和一个距离超平面100的点，明显是距离为0.1的点更有可能是负类别的点混入了边界。同理，一个距离超平面距离为-0.1的点，和一个离超平面距离为-100的点，明显是-100的点的标签更有可能是负类接口decision_function返回的值也因此被我们认为是SVM中的置信度(confidence)。

不过，置信度始终不是概率，它没有边界，可以无限大。大部分时候不是也小数的形式呈现，而SVC的判断过程又不像决策树一样求解出一个比例。为了解决这个矛盾，SVC有重要参数probability。

probability：是否启用概率估计，布尔值，可不填，默认时False。必须在调用fit之前使用它，启用此功能会减慢SVM的计算速度。设置为True会启动，SVC的接口predict_proba和predict_log_proba将生效。在二分类情况下，SVC将使用Platt缩放生成概率，即在decision_function生成的距离上进行Sigmoid压缩，并附加训练数据的交叉验证拟合，来生成类逻辑回归的SVM分数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs
class_1 = 500 #类别1有500个样本
class_2 = 50 #类别2只有50个
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [1.5, 0.5] #设定两个类别的方差，通常来说，样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False)
#看看数据集长什么样
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=10)
plt.show()
#其中红色点是少数类，紫色点是多数类
clf_proba = svm.SVC(kernel="linear",C=1.0,probability=True).fit(X,y)
print("返回预测某标签的概率：",clf_proba.predict_proba(X))
print("行数和列数：",clf_proba.predict_proba(X).shape)
print("每个样本到划分数据集的超平面的距离：",clf_proba.decision_function(X))

绘制SVM的ROC曲线

现在，我们理解了什么是阈值（threshold），了解了不同阈值会让混淆矩阵产生变化，也了解了如何从我们的分类算法中获取概率。现在，我们就可以开始画我们的ROC曲线了。ROC是一条以不同阈值下的假正率FPR为横坐标，不同阈值下的召回率Recall为纵坐标的曲线。简单地来说，只要我们有数据和模型，我们就可以在python中绘制出我们的ROC曲线。思考一下，我们要绘制ROC曲线，就必须在我们的数据中去不断调节阈值，不断求解混淆矩阵，然后不断获得我们的横坐标和纵坐标，最后才能够将曲线绘制出来。接下来，我们就来执行这个过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs
class_1 = 500 #类别1有500个样本
class_2 = 50 #类别2只有50个
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [1.5, 0.5] #设定两个类别的方差，通常来说，样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False)
#看看数据集长什么样
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=10)
plt.show()
from sklearn.metrics import confusion_matrix as CM
from sklearn.linear_model import LogisticRegression as LogiR
clf_lo=LogiR().fit(X,y)
prob=clf_lo.predict_proba(X)
import pandas as pd
prob=pd.DataFrame(prob)
prob.columns=["0","1"]
for i in range(prob.shape[0]):
    #将0.5设立为阈值
    if prob.loc[i,"1"] > 0.5:
    #创建了一个新的列名为pred的列
        prob.loc[i,"pred"] = 1
    else:
        prob.loc[i,"pred"] = 0
#创建了名为y_true的列，且将y赋值为该列
prob["y_true"] = y
prob = prob.sort_values(by="1",ascending=False)
cm = CM(prob.loc[:,"y_true"],prob.loc[:,"pred"],labels=[1,0])
#开始绘图
recall = []
FPR = []
clf_proba = svm.SVC(kernel="linear",C=1.0,probability=True).fit(X,y)
probrange = np.linspace(clf_proba.predict_proba(X)
[:,1].min(),clf_proba.predict_proba(X)[:,1].max(),num=50,endpoint=False)
from sklearn.metrics import confusion_matrix as CM, recall_score as R
import matplotlib.pyplot as plot
for i in probrange:
    y_predict = []
    for j in range(X.shape[0]):
        if clf_proba.predict_proba(X)[j,1] > i:
            y_predict.append(1)
        else:
            y_predict.append(0)
    cm = CM(y,y_predict,labels=[1,0])
    recall.append(cm[0,0]/cm[0,:].sum())
    FPR.append(cm[1,0]/cm[1,:].sum())
#排序
recall.sort()
FPR.sort()
plt.plot(FPR,recall,c="red")
plt.plot(probrange+0.05,probrange+0.05,c="black",linestyle="--")
plt.show()

运行后，得出下图：

我们建立ROC曲线的根本目的是找寻Recall和FPR之间的平衡，让我们能够衡量模型在尽量捕捉少数类的时候，误伤多数类的情况会如何变化。横坐标是FPR，代表着模型将多数类判断错误的能力，纵坐标Recall，代表着模型捕捉少数类的能力，所以ROC曲线代表着，随着Recall的不断增加，FPR如何增加。我们希望随着Recall的不断提升，FPR增加得越慢越好，这说明我们可以尽量高效地捕捉出少数类，而不会将很多地多数类判断错误。所以，我们希望看到的图像是，纵坐标急速上升，横坐标缓慢增长，也就是在整个图像左上方的一条弧线。这代表模型的效果很不错，拥有较好的捕获少数类的能力。

中间的虚线代表着，当recall增加1%，我们的FPR也增加1%，也就是说，我们每捕捉出一个少数类，就会有一个多数类被判错，这种情况下，模型的效果就不好，这种模型捕获少数类的结果，会让许多多数类被误伤，从而增加我们的成本。ROC曲线通常都是凸型的。对于一条凸型ROC曲线来说，曲线越靠近左上角越好，越往下越糟糕，曲线如果在虚线的下方，则证明模型完全无法使用。但是它也有可能是一条凹形的ROC曲线。对于一条凹型ROC曲线来说，应该越靠近右下角越好，凹形曲线代表模型的预测结果与真实情况完全相反，那也不算非常糟糕，只要我们手动将模型的结果逆转，就可以得到一条左上方的弧线了。最糟糕的就是，无论曲线是凹形还是凸型，曲线位于图像中间，和虚线非常靠近，那我们拿它无能为力。

现在，我们虽然拥有了这条曲线，但是还是没有具体的数字帮助我们理解ROC曲线和模型效果。接下来将AUC面加，它代表了ROC曲线下方的面积，这个面积越大，代表ROC曲线越接近左上角，模型就越好。

AUC面积

sklearn中，我们有帮助我们计算ROC曲线的横坐标假正率FPR，纵坐标Recall和对应的阈值的类
sklearn.metrics.roc_curve。同时，我们还有帮助我们计算AUC面积的类sklearn.metrics.roc_auc_score。

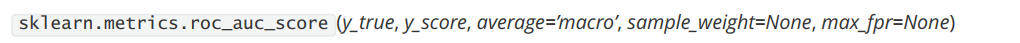
AUC面积的分数使用以上类来进行计算，输入的参数也比较简单，就是真实标签，和与roc_curve中一致的置信度分数或者概率值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sklearn.metrics import roc_curve
FPR, recall, thresholds = roc_curve(y,clf_proba.decision_function(X), pos_label=1)
#阈值可以也为负
print(FPR,recall,thresholds)
from sklearn.metrics import roc_auc_score as AUC
area = AUC(y,clf_proba.decision_function(X))
plt.figure()
plt.plot(FPR, recall, color='red',
label='ROC curve (area = %0.2f)' % area)
plt.plot([0, 1], [0, 1], color='black', linestyle='--')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('Recall')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

利用ROC曲线找出最佳阈值

对ROC曲线的理解来：ROC曲线反应的是recall增加的时候FPR如何变化，也就是当模型捕获少数类的能力变强的时候，会误伤多数类的情况是否严重。我们的希望是，模型在捕获少数类的能力变强的时候，尽量不误伤多数类，也就是说，随着recall的变大，FPR的大小越小越好。所以我们希望找到的最有点，其实是Recall和FPR差距最大的点。这个点，又叫做约登指数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
maxindex=(recall-FPR).tolist().index(max(recall-FPR))
#得出最佳阈值
print("最佳阈值：",thresholds[maxindex])
plt.scatter(FPR[maxindex],recall[maxindex],c="black",s=30)
plt.figure()
plt.plot(FPR, recall, color='red',
label='ROC curve (area = %0.2f)' % area)
plt.plot([0, 1], [0, 1], color='black', linestyle='--')
plt.scatter(FPR[maxindex],recall[maxindex],c="black",s=30)
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('Recall')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

这样，最佳阈值和最好的点都找了出来。

----本文结束，感谢您的阅读。如有错，请指正。----
大哥大嫂过年好！支持我一下呗
0%