非线性SVM与核函数
SVC在非线性数据上的推广
为了能够找出非线性数据的线性决策边界,我们需要将数据从原始的空间x投射到新空间Φ(x)中,Φ是一个映射函数,它代表了某种非线性的变换,如同我们之前所做过的使用r来升维一样,这种非线性变换看起来是一种非常有效的方式。使用这种变换,线性SVM的原理可以被很容易推广到非线性情况下,其推到过程核逻辑都与线性SVM一摸一样,只不过在第一决策边界之前,我们必须先对数据进行升维,即将原始的x转换成Φ。
重要参数kernel
这种变换非常巧妙,但也带有一些实现问题。首先,我们可能不清楚应该什么样的数据应该使用什么类型的映射函数来确保可以在变换空间中找出线性决策边界。极端情况下,数据可能会被映射到无限维度的空间中,这种高维空间可能不是那么友好,维度越多,推导和计算的难度都会随之暴增。其次,已知适当的映射函数,我们想要计算类似于Φ(x)i* Φ(xtest)这样的点积,计算量无法巨大。要找出超平面所付出的代价是非常昂贵的。
关键概念:核函数
而解决上面这些问题的数学方式,叫做”核技巧”。是一种能够使用数据原始空间中的向量计算来表示升维后的空间中的点积结果的数学方式。具体体现为,K(u,v)= Φ(u)*Φ(v)。而这个原始空间中的点积函数K(u,v),就被叫做“核函数”。
核函数能够帮助我们解决三个问题:
第一,有了核函数之后,我们无需去担心$\Phi$究竟应该是什么样,因为非线性SVM中的核函数都是正定核函数(positive definite kernel functions),他们都满足美世定律(Mercer’s theorem),确保了高维空间中任意两个向量的点积一定可以被低维空间中的这两个向量的某种计算来表示。
第二,使用核函数计算低维度中的向量关系比计算原来的Φ(xi) * Φ(xtest)要简单太多了。
第三,因为计算是在原始空间中进行,所以避免了维度诅咒的问题。
选用不同的核函数,就可以解决不同数据分布下的寻找超平面问题。在SVC中,这个功能由参数“kernel”和一系列与核函数相关的参数来进行控制。之前的代码中我们一直使用这个参数并输入”linear”,但却没有给大家详细讲解,也是因为如果不先理解核函数本身,很难说明这个参数到底在做什么。参数“kernel”在sklearn中可选以下几种选项:

可以看出,除了选项”linear”之外,其他核函数都可以处理非线性问题。多项式核函数有次数d,当d为1的时候它就是再处理线性问题,当d为更高次项的时候它就是在处理非线性问题。我们之前画图时使用的是选项“linear”,自然不能处理环形数据这样非线性的状况。而刚才我们使用的计算r的方法,其实是高斯径向基核函数所对应的功能,在参数”kernel“中输入”rbf“就可以使用这种核函数。
1 | from sklearn.svm import SVC |
运行后,从效果图可以看到,决策边界被完美的找了出来。
探索核函数在不同数据集上的表现
1 | import numpy as np |
可以观察到,线性核函数和多项式核函数在非线性数据上表现会浮动,如果数据相对线性可分,则表现不错,如果是像环形数据那样彻底不可分的,则表现糟糕。在线性数据集上,线性核函数和多项式核函数即便有扰动项也可以表现不错,可见多项式核函数是虽然也可以处理非线性情况,但更偏向于线性的功能。Sigmoid核函数就比较尴尬了,它在非线性数据上强于两个线性核函数,但效果明显不如rbf,它在线性数据上完全比不上线性的核函数们,对扰动项的抵抗也比较弱,所以它功能比较弱小,很少被用到。rbf,高斯径向基核函数基本在任何数据集上都表现不错,属于比较万能的核函数。我个人的经验是,无论如何先试试看高斯径向基核函数,它适用于核转换到很高的空间的情况,在各种情况下往往效果都很不错,如果rbf效果不好,那我们再试试看其他的核函数。另外,多项式核函数多被用于图像处理之中。
选取与核函数相关的参数

在知道如何选取核函数后,我们还要观察一下除了kernel之外的核函数相关的参数。对于线性核函数,”kernel”是唯一能够影响它的参数,但是对于其他三种非线性核函数,他们还受到参数gamma,degree以及coef0的影响。参数gamma就是表达式中的γ,degree就是多项式核函数的次数d,参数coef0就是常数项γ。其中,高斯径向基核函数受到gamma的影响,而多项式核函数受到全部三个参数的影响。

1 | #使用交叉验证得出最好的参数和准确率 |
重要参数C
关键概念:硬件隔与软件隔
当两组数据是完全线性可分,我们可以找出一个决策边界使得训练集上的分类误差为0,这两种数据就被称为是存在“硬间隔“的。当两组数据几乎是完全线性可分的,但决策边界在训练集上存在较小的训练误差,这两种数据就被称为是存在”软间隔“。

看上图,原来的决策边界ωx+b=0,原本的平行于决策边界的两个虚线超平面ω\x+b=1和ω*x+b=-1都依然有效。我们的原始判别函数是:

不过,这些超平面现在无法让数据上的训练误差等于0了,因为此时存在了一个混杂在红色点中的紫色点。于是,我们需要放松我们原始判别函数中的不等条件,来让决策边界能够适用于我们的异常点。于是我们引入松弛系数Φ来帮助我们优化原始的判别函数:
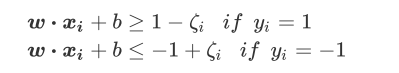
其中ζi>0。可以看的出,这其实是将原来的虚线超平面向图像的上方和下方平移。松弛系数其实蛮好理解的,看上图,在红色点附近的蓝色点在原本的判别函数中必定会被分为红色,所有一定会判断错。我们现在做一条与决策边界平行,且过蓝色点的直线ωxi+b=1- ζi(图中的蓝色虚线)。这条直线是由ω\xi+b=1平移得到,所以两条直线在纵坐标上的差异就是ζi。而点ωxi+b=1的距离就可以表示为 ζi*ω/||ω||,即ζi在ω方向上的投影。由于单位向量是固定的,所以ζi可以作为蓝色点在原始的决策边界上的分类错误的程度的表示。隔得越远,分的越错。注意:ζi并不是点到决策超平面的距离本身。
不难注意到,我们让ω*xi+b>=1-ζi作为我们的新决策超平面,是有一定的问题的。虽然我们把异常的蓝色点分类正确了,但我们同时也分错了一系列红色的点。所以我们必须在我们求解最大边际的损失函数中加上一个惩罚项,用来惩罚我们具有巨大松弛系数的决策超平面。我们的拉格朗日函数,拉格朗日对偶函数,也因此都被松弛系数改变。现在,我们的损失函数为

C是用来控制惩罚力度的系数
我们的拉格朗日函数为(其中$\mu$是第二个拉格朗日乘数)

需要满足的KKT条件为

拉格朗日对偶函数为
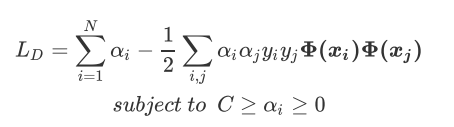
sklearn类SVC背后使用的最终公式。公式中现在唯一的新变量,松弛系数的惩罚力度C,由我们的参数C来进行控制。

在实际使用中,C和核函数的相关参数(gamma,degree等等)们搭配,往往是SVM调参的重点。与gamma不同,C没有在对偶函数中出现,并且是明确了调参目标的,所以我们可以明确我们究竟是否需要训练集上的高精确度来调整C的方向。默认情况下C为1,通常来说这都是一个合理的参数。 如果我们的数据很嘈杂,那我们往往减小C。当然,我们也可以使用网格搜索或者学习曲线来调整C的值。
1 | from sklearn.model_selection import StratifiedShuffleSplit |
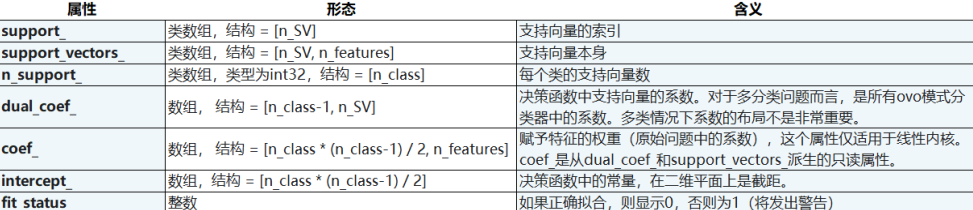
SVC的参数、属性和接口
参数



属性
接口


