XGBoost

前沿

在使用XGBoost之前，要先安装XGBoost库。xgboost库要求我们必须要提供适合的Scipy环境。以下为大家提供在windows中和MAC使用pip来安装xgboost的代码：

windows：

pip install xgboost #安装xgboost库
pip install —upgrade xgboost #更新xgboost库

我在这步遇到超时报错，查了以下，改成如下安装：

后面看到一些帖子，发现下面这个方法才是真的好用，在C:\Users\湛蓝星空 这个路径下创建一个pip文件夹，在文件夹创建一个txt，将下面内容加入文件里面，再将文件后缀名改为 .ini。

[global]
index-url = https://pypi.tuna.tsinghua.edu.cn/simple

这其实就是将源改为清华的源，防止被墙。非常管用

MAC：

brew install gcc@7
pip3 install xgboost

安装好XGBoost库后，我们有两种方式来使用我们的XGBoost库。第一种方式。是直接使用XGBoost库自己的建模流程。

其中最核心的，是DMtarix这个读取数据的类，以及train()这个用于训练的类。与sklearn把所有的参数都写在类中的方式不同，xgboost库中必须先使用字典设定参数集，再使用train来将参数及输入，然后进行训练。params可能的取值以及xgboost.train的列表：

我们也可以选择第二种方法，使用xgboost库中的sklearn的API：

有人发现，这两种方法的参数是不同的。其实只是写法不同，功能是相同的。使用xgboost中设定的建模流程来建模，和使用sklearnAPI中的类来建模，模型效果是比较相似的，但是xgboost库本身的运算速度（尤其是交叉验证）以及调参手段比sklearn要简单。

XGBoost

XGBoost本身的核心是基于梯度提升树实现的集成算法，整体来说可以有三个核心部分：集成算法本身，用于集成的弱评估器，以及应用中的其他过程。

梯度提升树

Boosting过程

XGBoost的基础是梯度提升算法，因此我们必须先从了解梯度提升算法开始。梯度提升（Gradient boosting）是构建预测模型的最强大技术之一，它是集成算法中提升法（Boosting）的代表算法。集成算法通过在数据上构建多个弱评估器，汇总所有弱评估器的建模结果，以获取比单个模型更好的回归或分类表现。弱评估器被定义为是表现至少比随机猜测更好的模型，即预测准确率不低于50%的任意模型。 集成不同弱评估器的方法有很多种。有像我们曾经在随机森林的课中介绍的，一次性建立多个平行独立的弱评估器的装袋法。也有像我们今天要介绍的提升法这样，逐一构建弱评估器，经过多次迭代逐渐累积多个弱评估器的方法。提升法的中最著名的算法包括Adaboost和梯度提升树，XGBoost就是由梯度提升树发展而来的。梯度提升树中可以有回归树也可以有分类树，两者都以CART树算法作为主流，XGBoost背后也是CART树，这意味着XGBoost中所有的树都是二叉的。

接下来，我们来了解一些Boosting算法是上面工作：首先，梯度提升回归树是专注于回归的树模型的提升集成模型，其建模过程大致如下：最开始先建立一棵树，然后逐渐迭代，每次迭代过程中都增加一棵树，逐渐形成众多树模型集成的强评估器。

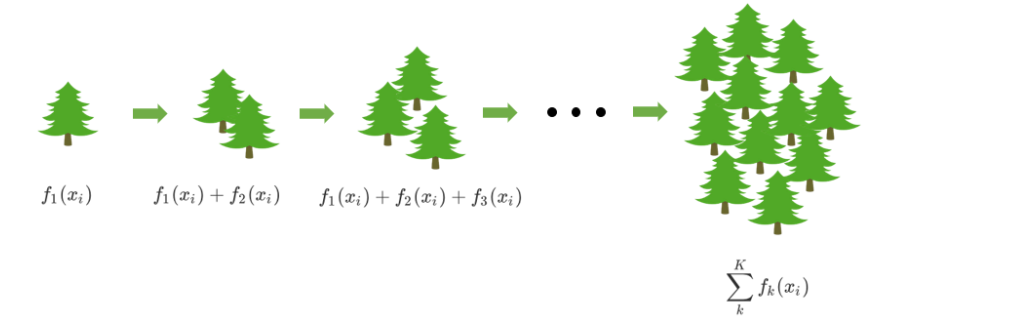
参数

from xgboost import XGBRegressor as XGBR
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.linear_model import LinearRegression as LinearR
from sklearn.datasets import load_boston
from sklearn.model_selection import KFold, cross_val_score as CVS, train_test_split as TTS
from sklearn.metrics import mean_squared_error as MSE
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = load_boston()
X = data.data
y = data.target
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
reg = XGBR(n_estimators=100).fit(Xtrain,Ytrain)
print("预测：",reg.predict(Xtest)) #传统接口predict
print("准确率：",reg.score(Xtest,Ytest))
print("均方误差：",MSE(Ytest,reg.predict(Xtest)))
print("模型的重要性分数：",reg.feature_importances_)

使用参数学习曲线观察n_estimators对模型的影响

axisx = range(10,1010,50)
cv = KFold(n_splits=5, shuffle = True, random_state=42)
rs = []
for i in axisx:
    reg = XGBR(n_estimators=i,random_state=420)
    rs.append(CVS(reg,Xtrain,Ytrain,cv=cv).mean())
print(axisx[rs.index(min(rs))],max(rs))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="red",label="XGB")
plt.legend()
plt.show()

方差与泛化误差

机器学习中，我们用来衡量模型在未知数据上的准确率的指标，叫做泛化误差（Genelization error）一个集成模型(f)在未知数据集(D)上的泛化误差 ，由方差(var)，偏差(bais)和噪声(ε)共同决定。其中偏差就是训练集上的拟合程度决定，方差是模型的稳定性决定，噪音是不可控的。而泛化误差越小，模型就越理想。

cv=KFold(n_splits=5,shuffle=True,random_state=42)
axisx = range(100,300,10)
rs = []
var = []
ge = []
for i in axisx:
    reg = XGBR(n_estimators=i,random_state=420)
    cvresult = CVS(reg,Xtrain,Ytrain,cv=cv)
    rs.append(cvresult.mean())
    var.append(cvresult.var())
    ge.append((1 - cvresult.mean())**2+cvresult.var())
#得出最好的n_estimators
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
rs = np.array(rs)
var = np.array(var)*0.01
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="black",label="XGB")
#添加方差线
plt.plot(axisx,rs+var,c="red",linestyle='-.')
plt.plot(axisx,rs-var,c="red",linestyle='-.')
plt.legend()
plt.show()
plt.figure(figsize=(20,5))
#泛化误差的可控部分
plt.plot(axisx,ge,c="gray",linestyle='-.')
plt.show()

从这个过程中观察n_estimators参数对模型的影响，我们可以得出以下结论：

首先，XGB中的树的数量决定了模型的学习能力，树的数量越多，模型的学习能力越强。只要XGB中树的数量足够 了，即便只有很少的数据， 模型也能够学到训练数据100%的信息，所以XGB也是天生过拟合的模型。但在这种情况 下，模型会变得非常不稳定。

第二，XGB中树的数量很少的时候，对模型的影响较大，当树的数量已经很多的时候，对模型的影响比较小，只能有 微弱的变化。当数据本身就处于过拟合的时候，再使用过多的树能达到的效果甚微，反而浪费计算资源。当唯一指标 或者准确率给出的n_estimators看起来不太可靠的时候，我们可以改造学习曲线来帮助我们。

第三，树的数量提升对模型的影响有极限，开始，模型的表现会随着XGB的树的数量一起提升，但到达某个点之 后，树的数量越多，模型的效果会逐步下降，这也说明了暴力增加n_estimators不一定有效果。
这些都和随机森林中的参数n_estimators表现出一致的状态。在随机森林中我们总是先调整n_estimators，当 n_estimators的极限已达到，我们才考虑其他参数，但XGB中的状况明显更加复杂，当数据集不太寻常的时候会更加 复杂。这是我们要给出的第一个超参数，因此还是建议优先调整n_estimators，一般都不会建议一个太大的数目， 300以下为佳。

subsample

我们训练模型之前，必然会有一个巨大的数据集。我们都知道树模型是天生过拟合的模型，并且如果数据量太过巨 大，树模型的计算会非常缓慢，因此，我们要对我们的原始数据集进行有放回抽样（bootstrap）。有放回的抽样每 次只能抽取一个样本，若我们需要总共N个样本，就需要抽取N次。每次抽取一个样本的过程是独立的，这一次被抽 到的样本会被放回数据集中，下一次还可能被抽到，因此抽出的数据集中，可能有一些重复的数据。在无论是装袋还是提升的集成算法中，有放回抽样都是我们防止过拟合。

在sklearn中，我们使用参数subsample来控制我们的随机抽样。在xgb和sklearn中，这个参数都默认为1且不能取到0，所以取值范围是(0,1]。这说明我们无法控制模型是否进行随机有放回抽样，只能控制抽样抽出来的样本量大概是多少。

eta or learning_rate

在逻辑回归中，我们自定义步长α来干涉我们的迭代速率，在XGB中看起来却没有这样的设置，但其实不然。在XGB
中，我们完整的迭代决策树的公式应该写作：

其中η读作”eta”，是迭代决策树时的步长（shrinkage），又叫做学习率（learning rate）。和逻辑回归中的α类似，η
越大，迭代的速度越快，算法的极限很快被达到，有可能无法收敛到真正的最佳。η越小，越有可能找到更精确的最
佳值，更多的空间被留给了后面建立的树，但迭代速度会比较缓慢。

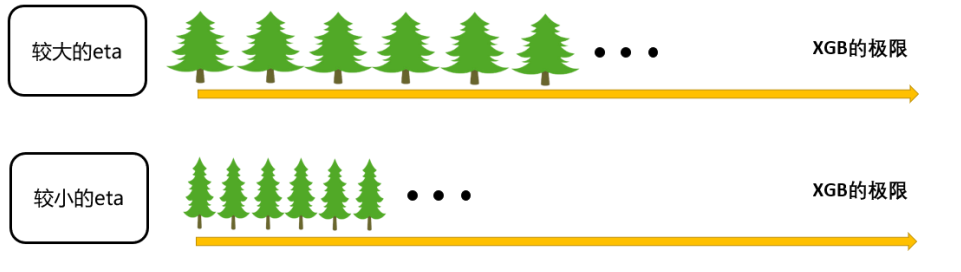
在sklearn中，我们使用参数learning_rate来干涉我们的学习速率：

梯度提升树是XGB的基础，本节中已经介绍了XGB中与梯度提升树的过程相关的四个参数：n_estimators，learning_rate ，silent，subsample。这四个参数的主要目的，其实并不是提升模型表现，更多是了解梯度提升树的原理。现在来看，我们的梯度提升树可是说是由三个重要的部分组成：

1. 一个能够衡量集成算法效果的，能够被最优化的损失函数
2. 一个能够实现预测的弱评估器
3. 一种能够让弱评估器集成的手段，包括我们讲解的迭代方法，抽样手段，样本加权等等过程

booster

梯度提升算法中不只有梯度提升树，XGB作为梯度提升算法的进化，自然也不只有树模型一种弱评估器。在XGB中，除了树模型，我们还可以选用线性模型，比如线性回归，来进行集成。虽然主流的XGB依然是树模型，但我们也可以使用其他的模型。基于XGB的这种性质，我们有参数“booster”来控制我们究竟使用怎样的弱评估器。

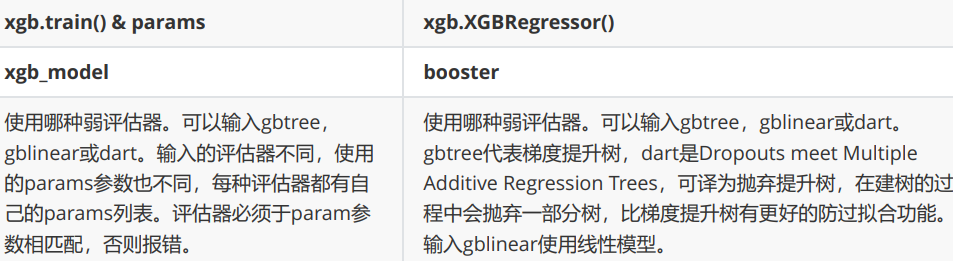
两个参数都默认为”gbtree”，如果不想使用树模型，则可以自行调整。当XGB使用线性模型的时候，它的许多数学过
程就与使用普通的Boosting集成非常相似。

for booster in ["gbtree","gblinear","dart"]:
reg = XGBR(n_estimators=180,learning_rate=0.1,random_state=420,booster=booster).fit(Xtrain,Ytrain)
	print(booster)
	print(reg.score(Xtest,Ytest))

objective

在众多机器学习算法中，损失函数的核心是衡量模型的泛化能力，即模型在未知数据上的预测的准确与否，我们训练模型的核心目标也是希望模型能够预测准确。在XGB中，预测准确自然是非常重要的因素，但我们之前提到过，XGB的是实现了模型表现和运算速度的平衡的算法。普通的损失函数，比如错误率，均方误差等，都只能够衡量模型的表现，无法衡量模型的运算速度。回忆一下，我们曾在许多模型中使用空间复杂度和时间复杂度来衡量模型的运算效率。XGB因此引入了模型复杂度来衡量算法的运算效率。因此XGB的目标函数被写作：传统损失函数 + 模型复杂度。

其中i代表数据集中的第i个样本，m表示导入第K棵树的数据总量，K代表建立的所有树(n_estimators)。 第二项代表模型的复杂度，使用树模型的某种变换$\Omega$表示，这个变化代表了一个从树的结构来衡量树模型的复杂度的式子,可以有多种定义。我们在迭代每一颗的过程中，都最小化Obj来求最优的yi。

在机器学习中，我们用来衡量模型在未知数据上的准确率的指标，叫做泛化误差（Genelization error）。一个集成模型(f)
在未知数据集(D)上的泛化误差 ，由方差(var)，偏差(bais)和噪声(ε)共同决定，而泛化误差越小，模型就越理想。从下面的图可以看出来，方差和偏差是此消彼长的，并且模型的复杂度越高，方差越大，偏差越小。

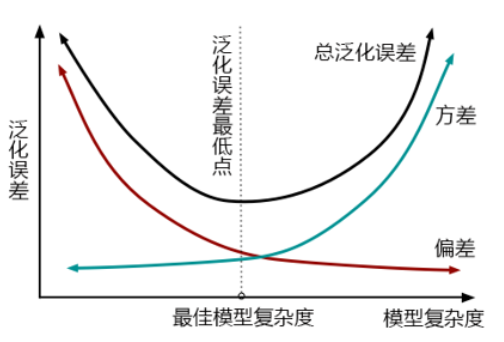
方差可以被简单地解释为模型在不同数据集上表现出来地稳定性，而偏差是模型预测的准确度。那方差-偏差困境就
可以对应到我们的Obj中了：

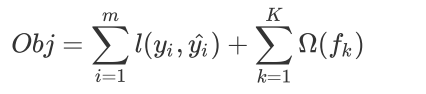
第一项是衡量我们的偏差，模型越不准确，第一项就会越大。第二项是衡量我们的方差，模型越复杂，模型的学习就会越具体，到不同数据集上的表现就会差异巨大，方差就会越大。所以我们求解Obj的最小值，其实是在求解方差与偏差的平衡点，以求模型的泛化误差最小，运行速度最快。

在应用中，我们使用参数“objective”来确定我们目标函数的第一部分，也就是衡量损失的部分。

xgb自身的调用方式：

from xgboost import XGBRegressor as XGBR
from sklearn.metrics import mean_squared_error as MSE
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split as TTS
data = load_boston()
X = data.data
y = data.target
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
#默认reg:linear
reg = XGBR(n_estimators=180,random_state=420).fit(Xtrain,Ytrain)
print("sklearn中的XGboost准确率：",reg.score(Xtest,Ytest))
print("sklearn中的xgb均方误差：",MSE(Ytest,reg.predict(Xtest)))
#xgb实现法
import xgboost as xgb
#使用类Dmatrix读取数据
dtrain = xgb.DMatrix(Xtrain,Ytrain)
dtest = xgb.DMatrix(Xtest,Ytest)
#写明参数，silent默认为False，通常需要手动将它关闭
param = {'silent':False,'objective':'reg:linear',"eta":0.1}
num_round = 180
#类train，可以直接导入的参数是训练数据，树的数量，其他参数都需要通过params来导入
bst = xgb.train(param, dtrain, num_round)
#接口predict
from sklearn.metrics import r2_score
print("xgb中的准确率：",r2_score(Ytest,bst.predict(dtest)))
print("xgb中的均方误差：",MSE(Ytest,bst.predict(dtest)))

看得出来，无论是从R²还是从MSE的角度来看，都是xgb库本身表现更优秀。

(alpha or reg_alpha) & (lambda or reg_lambda)

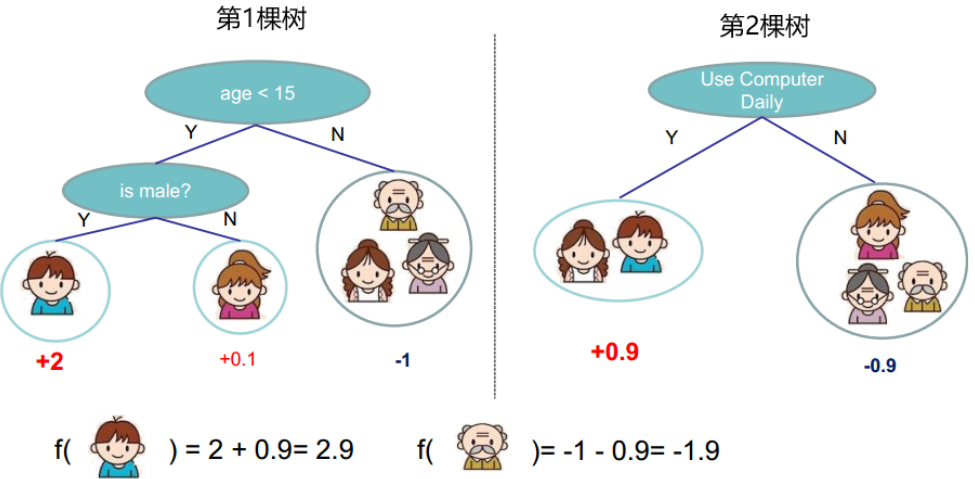
对于XGB来说，每个叶子节点上会有一个预测分数（prediction score），也被称为叶子权重。这个叶子权重就是所有在这个叶子节点上的样本在这一棵树上的回归取值,用f_k(x_i)或者ω来表示。

当有多棵树的时候，集成模型的回归结果就是所有树的预测分数之和，假设这个集成模型中总共有K棵决策树，则整
个模型在这个样本i上给出的预测结果为

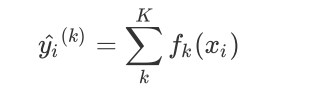
如下图：

设一棵树上总共包含了T个叶子节点，其中每个叶子节点的索引为j，则这个叶子节点上的样本权重是w_j。依据这个，我们定义模型的复杂度$\Omega$(f)为（注意这不是唯一可能的定义，我们当然还可以使用其他的定义，只要满足叶子越多/深度越大，复杂度越大的理论):

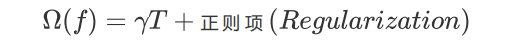
使用L2正则项：

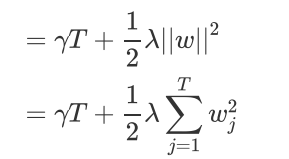
使用L1正则项：

还可以两个一起用：

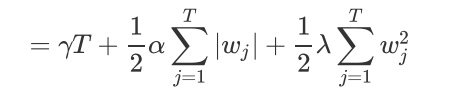
这个结构中有两部分内容，一部分是控制树结构的γ，另一部分则是我们的正则项。叶子数量T可以代表整个树结构，这是因为在XGBoost中所有的树都是CART树（二叉树），所以我们可以根据叶子的数量T判断出树的深度，而γ是我们自定的控制叶子数量的参数。 至于第二部分正则项，类比一下我们岭回归和Lasso的结构，参数α和λ的作用其实非常容易理解，他们都是控制正则化强度的参数，我们可以二选一使用，也可以一起使用加大正则化的力度。当 和 都为0的时候，目标函数就是普通的梯度提升树的目标函数。

来看正则化系数分别对应的参数：

gamma

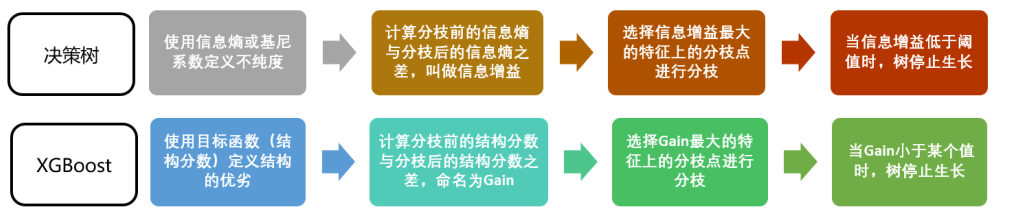
回忆一下决策树中我们是如何进行计算：我们使用基尼系数或信息熵来衡量分枝之后叶子节点的不纯度，分枝前的信息熵与分治后的信息熵之差叫做信息增益，信息增益最大的特征上的分枝就被我们选中，当信息增益低于某个阈值时，就让树停止生长。在XGB中，我们使用的方式是类似的：我们首先使用目标函数来衡量树的结构的优劣，然后让树从深度0开始生长，每进行一次分枝，我们就计算目标函数减少了多少，当目标函数的降低低于我们设定的某个阈值时，就让树停止生长。

原理还不是很明白，先贴最后的Gain函数

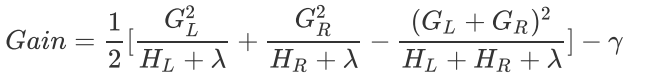
从上面的Gain函数，从上面的目标函数和结构分数之差Gain的式子来看，γ使我们每增加一片叶子就会被剪去的惩罚项。增加的叶子越多，结构分数之差Gain会被惩罚越重，所以γ也被称为”复杂性控制“。所以γ是我们用来防止过拟合的重要参数。γ是对梯度提升树影响最大的参数之一，其效果不逊色与n_estimators和放过拟合神器max_depth。同时γ还是我们让树停止生长的重要参数。

在XGB中，规定只要结构分数之差Gain大于0，即只要目标函数还能减小，我们就允许继续进行分枝。也就是说，我们对于目标函数减小量的要求是：

因此，我们可以直接通过设定γ的大小让XGB的树停止生长。γ因此被定义为，在树的叶节点上进行进一步分枝所需的最小目标函数减少量，在决策树和随机森林中也有类似的参数(min_split_loss，min_samples_split)。 设定越大，算法就越保守，树的叶子数量就越少，模型的复杂度就越低。

from xgboost import XGBRegressor as XGBR
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split as TTS
import numpy as np
from matplotlib import pyplot as plt
from sklearn.model_selection import cross_val_score as CVS
data = load_boston()
X = data.data
y = data.target
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
axisx = np.arange(0,5,0.05)
rs = []
var = []
ge = []
for i in axisx:
    reg = XGBR(n_estimators=180,random_state=420,gamma=i)
    result = CVS(reg,Xtrain,Ytrain,cv=20)
    rs.append(result.mean())
    var.append(result.var())
    ge.append((1 - result.mean())**2+result.var())
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
rs = np.array(rs)
var = np.array(var)*0.1
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="black",label="XGB")
plt.plot(axisx,rs+var,c="red",linestyle='-.')
plt.plot(axisx,rs-var,c="red",linestyle='-.')
plt.legend()
plt.show()

为了调整γ，我们需要引入新的工具，xgboost库中的类xgboost.cv

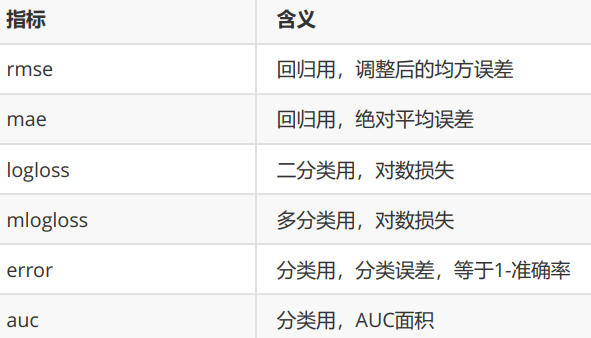
为了使用xgboost.cv，我们必须要熟悉xgboost自带的模型评估指标。xgboost在建库的时候本着大而全的目标，和sklearn类似，包括了大约20个模型评估指标，然而用于回归和分类的其实只有几个，大部分是用于一些更加高级的功能比如ranking。来看用于回归和分类的评估指标都有哪些：

from matplotlib import pyplot as plt
import xgboost as xgb
from sklearn.datasets import load_breast_cancer
data2 = load_breast_cancer()
x2 = data2.data
y2 = data2.target
dfull2 = xgb.DMatrix(x2,y2)
param1 = {'silent':True,'obj':'binary:logistic',"gamma":0,"nfold":5}
param2 = {'silent':True,'obj':'binary:logistic',"gamma":2,"nfold":5}
num_round = 100
cvresult1 = xgb.cv(param1, dfull2, num_round,metrics=("error"))
cvresult2 = xgb.cv(param2, dfull2, num_round,metrics=("error"))
plt.figure(figsize=(20,5))
plt.grid()
plt.plot(range(1,101),cvresult1.iloc[:,0],c="red",label="train,gamma=0")
plt.plot(range(1,101),cvresult1.iloc[:,2],c="orange",label="test,gamma=0")
plt.plot(range(1,101),cvresult2.iloc[:,0],c="green",label="train,gamma=2")
plt.plot(range(1,101),cvresult2.iloc[:,2],c="blue",label="test,gamma=2")
plt.legend()
plt.show()

scale_pos_weight

XGB中存在着调节样本不平衡的参数scale_pos_weight,这个参数非常类似于之前随机森林和支持向量机中我们都使用到过的class_weight参数。

其它参数

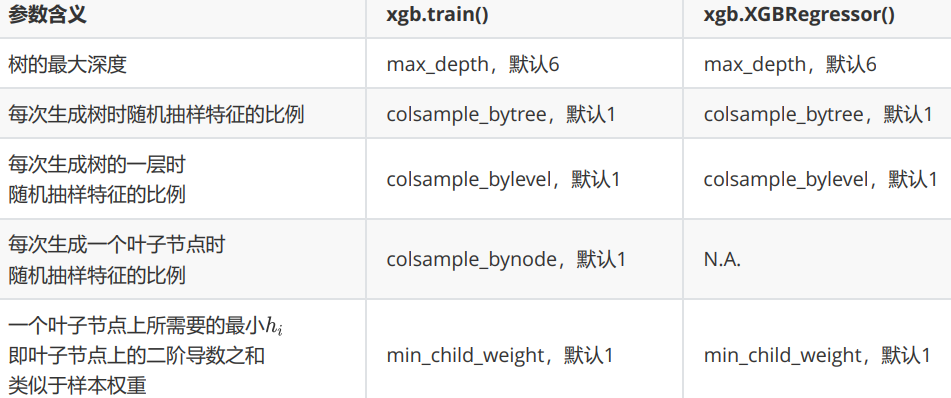
XGBoost应用的核心之一就是减轻过拟合带来的影响。作为树模型，减轻过拟合的方式主要是靠对决策树剪枝来降低模型的复杂度，以求降低方差。在之前的讲解中，我们已经学习了好几个可以用来防止过拟合的参数，包括上一节提到的复杂度控制λ，正则化的两个参数λ和α，控制迭代速度的参数 以及管理每次迭代前进行的随机有放回抽样的参数subsample。所有的这些参数都可以用来减轻过拟合。但除此之外，我们还有几个影响重大的，专用于剪枝的参数：

使用Pickle保存和调用模型

pickle是python编程中比较标准的一个保存和调用模型的库，我们可以使用pickle和open函数的连用，来讲我们的模型保存到本地。

#保存模型的coding
import pickle
import xgboost as xgb
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
data2 = load_breast_cancer()
x2 = data2.data
y2 = data2.target
Xtrain,Xtest,Ytrain,Ytest=train_test_split(x2,y2,test_size=0.3,random_state=420)
dtrain = xgb.DMatrix(Xtrain,Ytrain)
#设定参数，对模型进行训练
param = {'silent':True
,'obj':'reg:linear'
,"subsample":1
,"eta":0.05
,"gamma":20
,"lambda":3.5
,"alpha":0.2
,"max_depth":4
,"colsample_bytree":0.4
,"colsample_bylevel":0.6
,"colsample_bynode":1}
num_round = 180
bst = xgb.train(param, dtrain, num_round)
#保存模型
pickle.dump(bst, open("xgboostonboston.dat","wb"))

#调用模型的coding
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split as TTS
from sklearn.metrics import mean_squared_error as MSE
import pickle
import xgboost as xgb
data = load_breast_cancer()
X = data.data
y = data.target
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
#注意，如果我们保存的模型是xgboost库中建立的模型，则导入的数据类型也必须是xgboost库中的数据类型
dtest = xgb.DMatrix(Xtest,Ytest)
#导入模型
loaded_model = pickle.load(open("xgboostonboston.dat", "rb"))
print("Loaded model from: xgboostonboston.dat")
#做预测
ypreds = loaded_model.predict(dtest)
from sklearn.metrics import mean_squared_error as MSE, r2_score
print("均方误差：",MSE(Ytest,ypreds))
print(r2_score(Ytest,ypreds))

使用Joblib保存和调用模型

Joblib是SciPy生态系统中的一部分，它为Python提供保存和调用管道和对象的功能，处理NumPy结构的数据尤其高
效，对于很大的数据集和巨大的模型非常有用。Joblib与pickle API非常相似

from xgboost import XGBRegressor as XGBR
bst = XGBR(n_estimators=200,eta=0.05,gamma=20,reg_lambda=3.5,reg_alpha=0.2,max_depth=4,colsample_bytree=0.4,colsample_bylevel=0.6).fit(Xtrain,Ytrain)
#保存模型
joblib.dump(bst,"xgboost-boston.dat")
#调用模型
loaded_model = joblib.load("xgboost-boston.dat")
#这里可以直接导入Xtest
ypreds = loaded_model.predict(Xtest)
print（MSE(Ytest, ypreds)）