线性回归

线性回归原理

回归是一种应用广泛的预测建模技术，这种技术的核心在于预测的结果是连续型变量。决策树，随机森林，支持向
量机的分类器等分类算法的预测标签是分类变量，多以{0，1}来表示，而无监督学习算法比如PCA，KMeans的目
标根本不是求解出标签，注意加以区别。

线性回归的类可能是我们目前为止学到的最简单的类，仅有四个参数就可以完成一个完整的算法。并且看得出，这
些参数中并没有一个是必填的，更没有对我们的模型有不可替代作用的参数。这说明，线性回归的性能，往往取决
于数据本身，而并非是我们的调参能力，线性回归也因此对数据有着很高的要求。幸运的是，现实中大部分连续型
变量之间，都存在着或多或少的线性联系。所以线性回归虽然简单，却很强大。顺便一提，sklearn中的线性回归
可以处理多标签问题，只需要在fit的时候输入多维度标签就可以了。

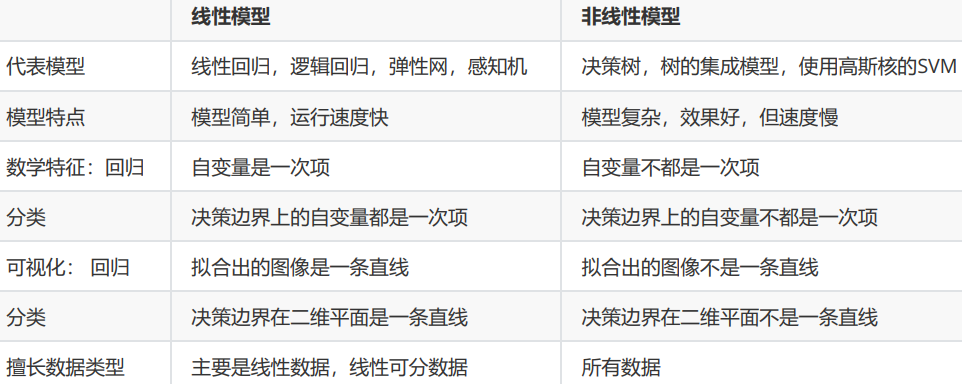
线性回归是机器学习中最简单的回归算法，多元线性回归指的就是一个样本有多个特征的线性回归问题。对于一个
有n个特征的样本i而言，它的回归结果可以写作一个几乎人人熟悉的方程 ：

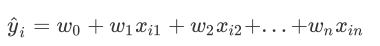
ω被统称为模型的参数。ω0被称为截距ω₁~ω_n被称为回归系数。这个表达式，其实就和我们小学时就无比熟悉的y=ax+b是同样的性质。其中y是我们的目标变量，也就是标签。 X_i1-X_in是样本i上的特征不同特征。如果考虑我们有m个样本，则m个样本的回归结果可以被写作：

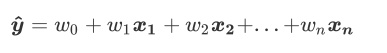
我们可以使用矩阵来表示这个方程：

y=Xω，其中y是包含了m个全部的样本的回归结果的列向量。粗体的大写字母表示矩阵。我们可以使用矩阵来表示这个方程，其中ω可以被看做是一个结构为(1,n)的列矩阵，X是一个结构为(m,n)的特征矩阵。这个预测函数的本质就是我们需要构建的模型，而构造预测函数的核心就是找出模型的参数向量ω。

在多元线性回归中，我们在损失函数如下定义：

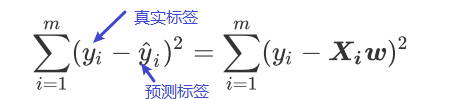
在这个平方结果下，我们的真实标签和预测值分别如上图表示，也就是说，这个损失函数是在计算我们的真实标签和预测值之间的距离。因此，我们认为这个损失函数衡量了我们构造的模型的预测结果和真实标签的差异，因此我们固然希望我们的预测结果和真实值差异越小越好。所以我们的求解目标就可以转化成 ：

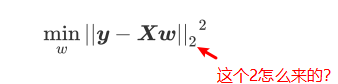
第一次看不明白上面红字，后面看了书，才明白。这个2表示L2范式。也就是我们损失函数代表的含义，在L2范式上开平方，就是我们的损失函数。上面这个式子，正是sklearn当中，用在类Linear_model.LinerRegression背后使用的损失函数，我们往往称呼这个式子为SSE(残差平方和)或RSS(误差平方和)。

现在问题转换成了求解让RSS最小化的参数向量 ，这种通过最小化真实值和预测值之间的RSS来求解参数的方法叫做最小二乘法。接下来，我们对ω求导。

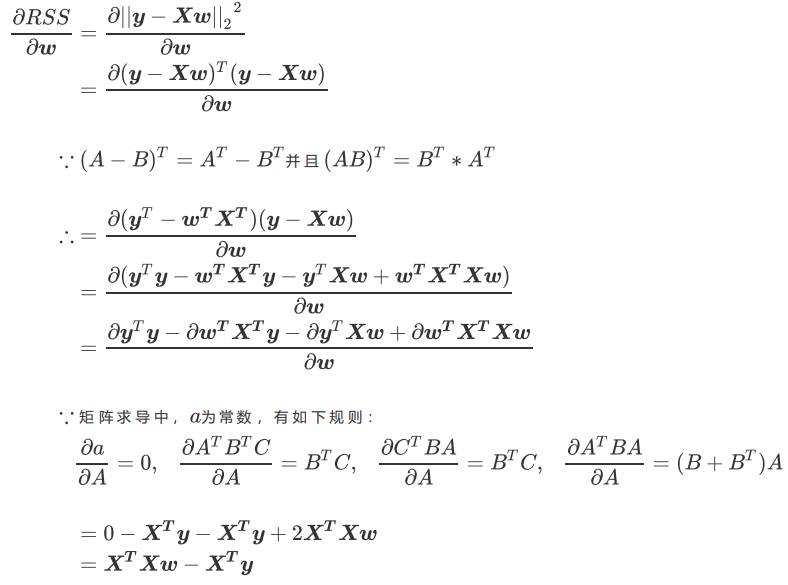
我们让求导后的一阶导数为0，并且我们的特征矩阵X肯定不会是一个所有元素都为0的矩阵。得：

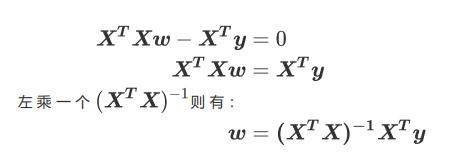
线性回归API

sklearn中的线性模型模块是linear_model。

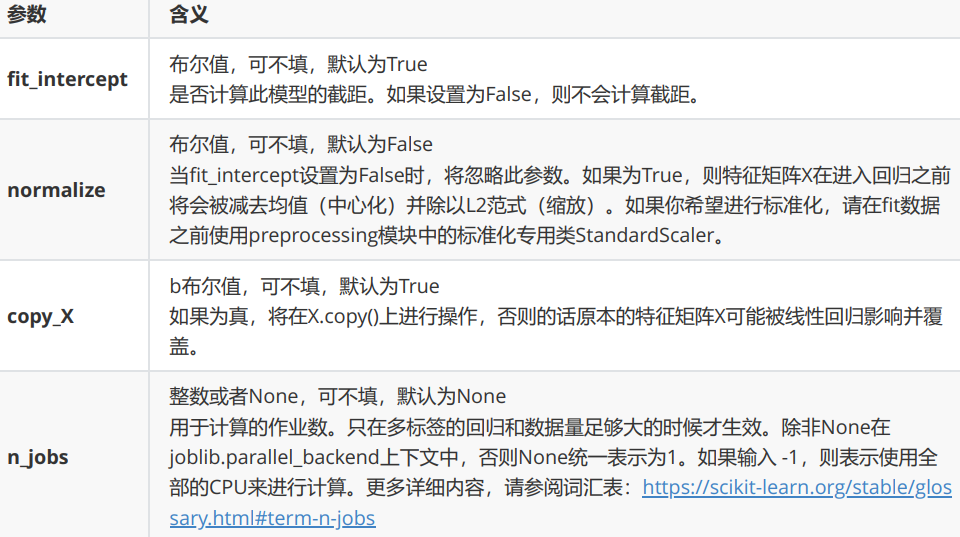
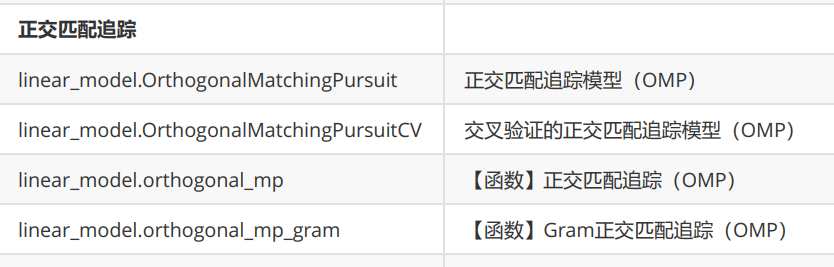
coding：

模型评估指标

回归类算法的模型评估一直都是回归算法中的一个难点，但不像我们曾经讲过的无监督学习算法中的轮廓系数等等
评估指标，回归类与分类型算法的模型评估其实是相似的法则——找真实标签和预测值的差异。只不过在分类型算
法中，这个差异只有一种角度来评判，那就是是否预测到了正确的分类，而在我们的回归类算法中，我们有两种不
同的角度来看待回归的效果：这两种角度，分别对于着不同得模型评估指标。
第一，我们是否预测到了正确的数值。
第二，我们是否拟合到了足够的信息。

sklearn当中，我们有两种方式调用这个评估指标，一种是使用sklearn专用的模型评估模块metrics里的类mean_squared_error，另一种是调用交叉验证的类cross_val_score并使用里面的scoring参数来设置使用均方误差

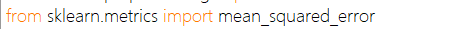
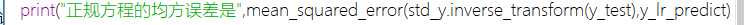
​ 注：y_lr_predict表示std_y.inverse_transform(ypredict),也就是预测得最终价格

from sklearn.linear_model import LinearRegression as LR
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import cross_val_score
from sklearn.metrics import mean_squared_error
from sklearn.datasets import fetch_california_housing as fch
housevalue=fch()
xtrain,xtest,ytrain,ytest=train_test_split(housevalue.data,housevalue.target,test_size=0.3,random_state=420)
std_x=StandardScaler()
xtrain=std_x.fit_transform(xtrain)
xtest=std_x.transform(xtest)
std_y=StandardScaler()
ytrain=std_y.fit_transform(ytrain.reshape(-1,1))
ytest=std_y.transform(ytest.reshape(-1,1))
reg=LR().fit(xtrain,ytrain)
ypredict=reg.predict(xtest)
print(std_y.inverse_transform(ypredict))
print("均方误差：",mean_squared_error(std_y.inverse_transform(ytest),std_y.inverse_transform(ypredict)))
print(cross_val_score(reg,housevalue.data,housevalue.target,cv=10,scoring="mean_squared_error"))

这里如果我们运行上面的代码，会在第十九行报错：

我们在决策树和随机森林中都提到过，虽然均方误差永远为正，但是sklearn中的参数scoring下，均方误差作为评
判标准时，却是计算”负均方误差“（neg_mean_squared_error）。这是因为sklearn在计算模型评估指标的时候，
会考虑指标本身的性质，均方误差本身是一种误差，所以被sklearn划分为模型的一种损失(loss)。在sklearn当中，
所有的损失都使用负数表示，因此均方误差也被显示为负数了。真正的均方误差MSE的数值，其实就是
neg_mean_squared_error去掉负号的数字。 我们可以将scoring改为”neg_mean_absolute_error” 。

print(cross_val_score(reg,housevalue.data,housevalue.target,cv=10,scoring="neg_mean_squared_error"))

为了衡量模型对数据上的信息量的捕捉，我们定义了R^2和可解释性方差分数(explained_variance_score，EVS)来帮助:

在R^2和EVS中，分子是真实值和预测值之差的差值，也就是我们的模型没有捕获到的信息总量，分母是真实标签所带的信息量，所以两者都衡量1-我们的模型没有捕获到的信息量占真实标签中所带的信息量的比例，所以，两者都是越接近1越好。

R^2我们也可以使用三种方式来调用，一种是直接从metrics中导入r2_score，输入预测值和真实值后打分。第二种
是直接从线性回归LinearRegression的接口score来进行调用。第三种是在交叉验证中，输入”r2”来调用。EVS有两
种调用方法，可以从metrics中导入，也可以在交叉验证中输入”explained_variance“来调用 。

print("R2",r2_score(ypredict,ytest))
print(reg.score(xtest,ytest))

????为什么结果不一样呢？然而看R2的计算公式，R2明显和分类模型的指标中的accuracy或者precision不一样，R2涉及到的计算中对预测值和真实值有极大的区别，必须是预测值在分子，真实值在分母。所以我们在调用metrcis模块中的模型评估指标的时候，必须要检查清楚，指标的参数中，究竟是要求我们先输入真实值还是先输入预测值 。所以我们要指定参数：

#直接用r2_score
print("R2",r2_score(y_true=ytest,y_pred=ypredict))
#利用接口score
print(reg.score(xtest,ytest))

#EVS的两种调用方法
from sklearn.metrics import explained_variance_score as evs
#第一种
print(cross_val_score(reg,housevalue.data,housevalue.target,cv=10,scoring="explained_variance"))
#第二种
print("evs",evs(ytest,ypredict))

多重共线性

矩阵A中第一行和第三行的关系，被称为“精确相关关系”，即完全相关，一行可使另一行为0。在这种精确相关关系下，矩阵A的行列式为0，则矩阵A的逆不可能存在。在我们的最小二乘法中，如果矩阵中存在这种精确相关关系，则逆不存在，最小二乘法完全无法使用，线性回归会无法求出结果。

矩阵B中第一行和第三行的关系不太一样，他们之间非常接近于”精确相关关系“，但又不是完全相关，一行不能使另一行为0，这种关系被称为”高度相关关系“。在这种高度相关关系下，矩阵的行列式不为0，但是一个非常接近0数，矩阵A的逆存在，不过接近于无限大。在这种情况下，最小二乘法可以使用，不过得到的逆会很大，直接影响我们对参数向量w的求解：

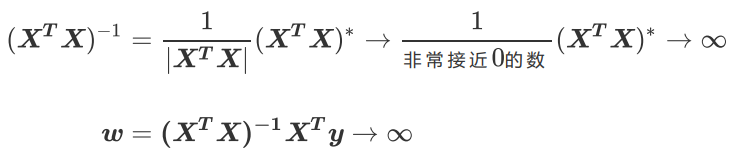
这样求解出来的参数向量w会很大，因此会影响建模的结果，造成模型有偏差或者不可用。精确相关关系和高度相关关系并称为”多重共线性”。在多重共线性下，模型无法建立，或者模型不可用。

相对的，矩阵C的行之间结果相互独立，梯形矩阵看起来非常正常，它的对角线上没有任何元素特别接近于0，因此其行列式也就不会接近0或者为0，因此矩阵C得出的参数向量w就不会有太大偏差，对于我们拟合而言是比较理想的。

从上面的所有过程我们可以看得出来，一个矩阵如果要满秩，则要求矩阵中每个向量之间不能存在多重共线性。这也构成了线性回归算法对于特征矩阵的要求。

多重共线性与相关性

多重共线性如果存在，则线性回归就无法使用最小二乘法来进行求解，或者求解就会出现偏差。幸运的是，不能存在
多重共线性，不代表不能存在相关性——机器学习不要求特征之间必须独立，必须不相关，只要不是高度相关或者精
确相关就好。

关键概念：多重共线性与相关性

多重共线性是一种统计现象，是指线性模型中的特征（解释变量）之间由于存在精确相关关系或高度相关关系，多重共线性的存在会使模型无法建立，或者估计失真。多重共线性使用指标方差膨胀因子（variance inflation factor，VIF）来进行衡量（from statsmodels.stats.outliers_influence import variance_inflation_factor），通常当我们提到“共线性”，都特指多重共线性。

相关性是衡量两个或多个变量一起波动的程度的指标，它可以是正的，负的或者0。当我们说变量之间具有相关性，通常是指线性相关性，线性相关一般由皮尔逊相关系数进行衡量，非线性相关可以使用斯皮尔曼相关系数或者互信息法进行衡量。

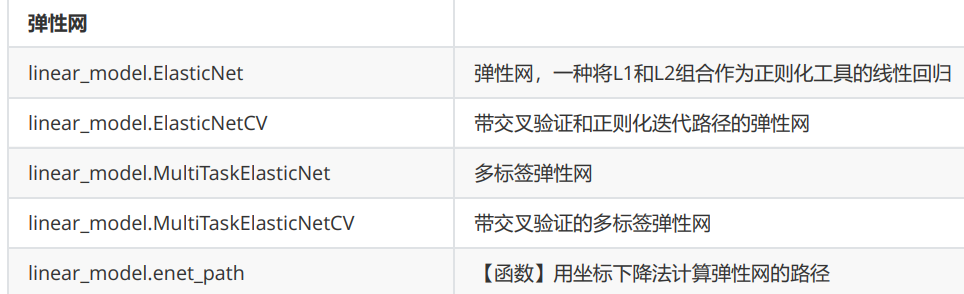
处理多重共线性的方法

这三种手段中，第一种相对耗时耗力，需要较多的人工操作，并且会需要混合各种统计学中的知识和检验来进行使
用。第二种手段在现实中应用较多，不过由于理论复杂，效果也不是非常高效。我们的核心是使用第三种方法：改进线性回归来处理多重共线性。为此，岭回归、Lasso、弹性网就被研究出来了。

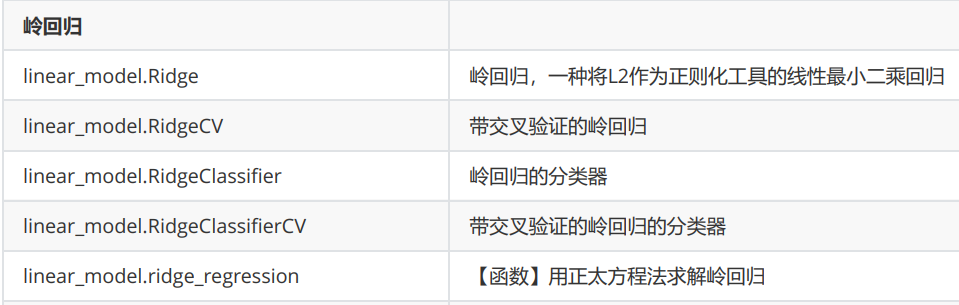
岭回归

在线性模型之中，除了线性回归之外，最知名的就是岭回归与Lasso了。这两个算法非常神秘，他们的原理和应用都不像其他算法那样高调，学习资料也很少。这可能是因为这两个算法不是为了提升模型表现，而是为了修复漏洞而设计的。

岭回归在多元线性回归的损失函数上加上了正则项，表达为系数w的L2范式（即系数w的平方项）乘以正则化系数α。岭回归的损失函数的完整表达式写作：

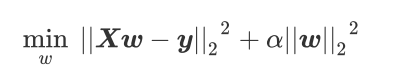
linear_model.Ridge

在sklearn中，岭回归由线性模型库中的Ridge类来调用

和线性回归相比，岭回归的参数稍微多了那么一点点，但是真正核心的参数就是我们的正则项的系数α ，其他的参数是当我们希望使用最小二乘法之外的求解方法求解岭回归的时候才需要的，通常我们完全不会去触碰这些参数。所以,大家只需要了解α的用法就可以了。

import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge, LinearRegression, Lasso
from sklearn.model_selection import train_test_split as TTS
from sklearn.datasets import fetch_california_housing as fch
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
housevalue = fch()
X = pd.DataFrame(housevalue.data)
#print(housevalue.data)
print(X.head())
y = housevalue.target
X.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目"
,"平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
#数据集索引恢复
print(Xtest.shape[0])
for i in [Xtrain,Xtest]:
    i.index = range(i.shape[0])
#使用岭回归来进行建模
reg = Ridge(alpha=1).fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest)
alpharange = np.arange(1,1001,100)
ridge, lr = [], []
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()
    linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()

运行上面代码，可以看出，加利佛尼亚数据集上，岭回归的结果轻微上升，随后骤降。可以说，加利佛尼亚房屋价值数据集带有很轻微的一部分共线性，这种共线性被正则化参数 消除后，模型的效果提升了一点点，但是对于整个模型而言是杯水车薪。在过了控制多重共线性的点后，模型的效果飞速下降，显然是正则化的程度太重，挤占了参数 本来的估计空
间。从这个结果可以看出，加利佛尼亚数据集的核心问题不在于多重共线性，岭回归不能够提升模型表现。

#观察模型方差
alpharange = np.arange(1,1001,100)
ridge, lr = [], []
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    varR = cross_val_score(reg,X,y,cv=5,scoring="r2").var()
    varLR = cross_val_score(linear,X,y,cv=5,scoring="r2").var()
    ridge.append(varR)
    lr.append(varLR)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Variance")
plt.legend()
plt.show()

可以发现，模型的方差上升快速。虽然岭回归和Lasso不是设计来提升模型表现，而是专注于解决多重共线性问题的，但当α在一定范围内变动的时候，消除多重共线性也许能够一定程度上提高模型的泛化能力。 不是很明白这句话，后面补

选取最佳的正则化参数

既然要选择α的范围，我们就不可避免的进行最优参数的选择。在各种机器学习教材中，总是教导使用岭迹图来判断正则项参数的最佳取值。传统的岭迹图长成下图：

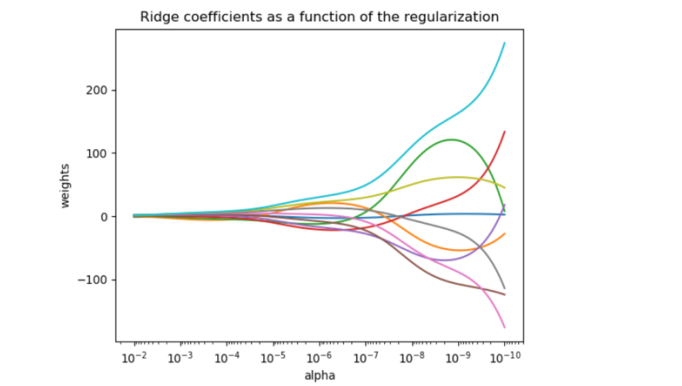
这一个以正则化参数为横坐标，线性模型求解的系数α为纵坐标的图像，其中每一条彩色的线都是一个系数α。其目标是建立正则化参数与系数α之间的直接关系，以此来观察正则化参数的变化如何影响了系数w的拟合。岭迹图认为，线条交叉越多，则说明特征之间的多重共线性越高。我们应该选择系数较为平稳的喇叭口所对应的α取值作为最佳的正则化参数的取值。绘制岭迹图的方法非常简单，代码如下:

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
#创造10*10的希尔伯特矩阵
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)
#计算横坐标
n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
coefs = []
for a in alphas:
    ridge = linear_model.Ridge(alpha=a, fit_intercept=False)
    ridge.fit(X, y)
    coefs.append(ridge.coef_)
#绘图展示结果
ax = plt.gca()
ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1]) #将横坐标逆转
plt.xlabel('正则化参数alpha')
plt.ylabel('系数w')
plt.title('岭回归下的岭迹图')
plt.axis('tight')
plt.show()

我非常不建议大家使用岭迹图来作为寻找最佳参数的标准。
有这样的两个理由：

1、岭迹图的很多细节，很难以解释。比如为什么多重共线性存在会使得线与线之间有很多交点？当α很大了之后看上去所有的系数都很接近于0，难道不是那时候线之间的交点最多吗？

2、岭迹图的评判标准，非常模糊。哪里才是最佳的喇叭口？哪里才是所谓的系数开始变得”平稳“的时候？一千个读者一千个哈姆雷特的画像？未免也太不严谨了

我们应该使用交叉验证来选择最佳的正则化系数。在sklearn中，我们有带交叉验证的岭回归可以使用：

RidgeCV的重要参数、属性和接口：

import numpy as np
import pandas as pd
from sklearn.linear_model import RidgeCV, LinearRegression
from sklearn.datasets import fetch_california_housing as fch
housevalue = fch()
X = pd.DataFrame(housevalue.data)
y = housevalue.target
X.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目"
,"平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]
Ridge_ = RidgeCV(alphas=np.arange(1,1001,100),store_cv_values=True).fit(X, y)
#无关交叉验证的岭回归结果
print("没有交叉验证的岭回归：",Ridge_.score(X,y))
#调用所有交叉验证的结果
print("调用所有交叉验证：",Ridge_.cv_values_.shape)
#进行平均后可以查看每个正则化系数取值下的交叉验证结果
print("平均后的每个正则化系数交叉验证结果：",max(Ridge_.cv_values_.mean(axis=0)))
#查看被选择出来的最佳正则化系数
print("最佳正则化系数：",Ridge_.alpha_)

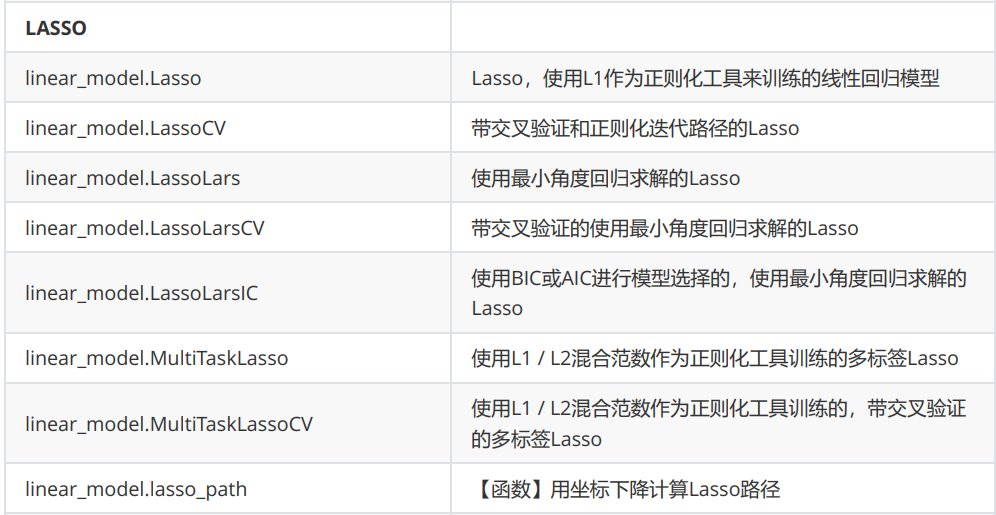
Lasso

除了岭回归之外，最常被人们提到还有模型Lasso。Lasso全称最小绝对收缩和选择算子（least absolute shrinkage and selection operator），由于这个名字过于复杂所以简称为Lasso。和岭回归一样，Lasso是被创造来作用于多重共线性问题的算法，不过Lasso使用的是系数w的L1范式（L1范式则是系数w的绝对值）乘以正则化系数α ，所以,Lasso的损失函数表达式为：

岭回归VSLasso：岭回归可以解决特征间的精确相关关系导致的最小二乘法无法使用的问题，而Lasso不行。

Lasso不是从根本上解决多重共线性问题，而是限制多重共线性带来的影响。

Lasso的核心作用：特征选择

sklearn中我们使用类Lasso来调用lasso回归，众多参数中我们需要比较在意的就是参数α ，正则化系数。另外需要注意的就是参数positive。当这个参数为”True”的时候，是我们要求Lasso回归出的系数必须为正数，以此来保证我们的α一定以增大来控制正则化的程度。 需要注意的是，在sklearn中我们的Lasso使用的损失函数是：

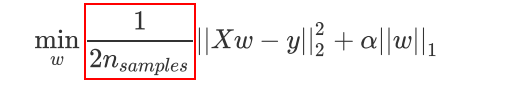
红色框框住的只是作为系数存在。用来消除我们对损失函数求导后多出来的那个2的（求解w时所带的1/2），然后对整体的RSS求了一个平均而已，无论时从损失函数的意义来看还是从Lasso的性质和功能来看，这个变化没有造成任何影响，只不过计算上会更加简便一些。

import pandas as pd
from sklearn.linear_model import Ridge, LinearRegression, Lasso
from sklearn.model_selection import train_test_split as TTS
from sklearn.datasets import fetch_california_housing as fch
import matplotlib.pyplot as plt
housevalue = fch()
X = pd.DataFrame(housevalue.data)
y = housevalue.target
X.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目"
,"平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
#恢复索引
for i in [Xtrain,Xtest]:
    i.index = range(i.shape[0])
#线性回归进行拟合
reg = LinearRegression().fit(Xtrain,Ytrain)
print("线性回归：",(reg.coef_*100).tolist())
#岭回归进行拟合
Ridge_ = Ridge(alpha=0).fit(Xtrain,Ytrain)
print("岭回归：",(Ridge_.coef_*100).tolist())
#Lasso进行拟合
lasso_ = Lasso(alpha=0).fit(Xtrain,Ytrain)
print("Lasso",(lasso_.coef_*100).tolist())

可以看到，岭回归没有报出错误，但Lasso就不一样了，虽然依然对系数进行了计算，但是报出了整整三个警告：

这三条分别是这样的内容：

​ 1、正则化系数为0，这样算法不可收敛！如果你想让正则化系数为0，请使用线性回归吧

​ 2、没有正则项的坐标下降法可能会导致意外的结果，不鼓励这样做！

​ 3、目标函数没有收敛，你也许想要增加迭代次数，使用一个非常小的alpha来拟合模型可能会造成精确度问题！

sklearn不推荐我们使用0这样的正则化系数。如果我们的确希望取到0，那我们可以使用一个比较很小的数，比如0.01这样的值：

#岭回归拟合
Ridge_ = Ridge(alpha=0.01).fit(Xtrain,Ytrain)
print((Ridge_.coef_*100).tolist())
#Lasso进行拟合
lasso_ = Lasso(alpha=0.01).fit(Xtrain,Ytrain)
print((lasso_.coef_*100).tolist())

这样就不会报任何警告了。

选取最佳的正则化

from sklearn.linear_model import LassoCV
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.datasets import fetch_california_housing as fch
import numpy as np
housevalue=fch()
Xtrain,Xtest,Ytrain,Ytest=train_test_split(housevalue.data,housevalue.target,test_size=0.3,random_state=420)
#自己建立Lasso进行alpha选择的范围
alpharange = np.logspace(-10, -2, 200,base=10)
lasso_ = LassoCV(alphas=alpharange #自行输入的alpha的取值范围
,cv=5 #交叉验证的折数
).fit(Xtrain, Ytrain)
#查看被选择出来的最佳正则化系数
print("最佳的正则化系数：",lasso_.alpha_)
#调用所有交叉验证的结果
print("所有交叉验证的结果：",lasso_.mse_path_)
print(lasso_.mse_path_.shape) #返回每个alpha下的五折交叉验证结果
print(lasso_.mse_path_.mean(axis=1)) #有注意到在岭回归中我们的轴向是axis=0吗？
#在岭回归当中我们的交叉验证结果返回的是，每一个样本在每个alpha下的交叉验证结果
#因此我们要求每个alpha下的交叉验证均值，就是axis=0，跨行求均值
#而在这里，我们返回的是，每一个alpha取值下，每一折交叉验证的结果
#因此我们要求每个alpha下的交叉验证均值，就是axis=1，跨列求均值
#最佳正则化系数下获得的模型的系数结果
print("最佳正则化系数获得的模型结果：",lasso_.coef_)
print("最佳正则化系数的准确率：",lasso_.score(Xtest,Ytest))
#与线性回归相比如何？
reg = LinearRegression().fit(Xtrain,Ytrain)
print("线性回归的准确率：",reg.score(Xtest,Ytest))
#使用lassoCV自带的正则化路径长度和路径中的alpha个数来自动建立alpha选择的范围
ls_ = LassoCV(eps=0.00001
,n_alphas=300
,cv=5
).fit(Xtrain, Ytrain)
print(ls_.alpha_)
print(ls_.alphas_) 
print(ls_.alphas_.shape)
print(ls_.score(Xtest,Ytest))
print(ls_.coef_)

模型效果上表现和普通的Lasso没有太大的区别，不过他们都在各个方面对原有的Lasso做了一些相应的改进（比如说提升了本来就已经很快的计算速度，增加了模型选择的维度，因为均方误差作为损失函数只考虑了偏差，不考虑方差的在。除了解决多重共线性这个核心问题之外，线性模型还有更重要的事情要做：提升模型表现。这才是机器学习最核心的需求，而Lasso和岭回归不是为此而设计的。为了提升模型表现而做出的改进：多项式回归。

多项式回归

首先，“线性”这个词用于描述不同事物时有着不同的含义，我们最常使用的线性是指“变量之间的线性关系(linear relationship)”。它表示两个变量之间的关系可以展示为一条直线，即可以使用方程y=ax+b来进行拟合。要探索两个变量之间的关系是否线性，最简单的方式就是绘制散点图，如果散点图能够相对均匀地分布在一条直线的两端，则说明这两个变量之间的关系是线性的。从线性关系这个概念出发，我们有了一种说法叫做“线性数据”。通常来说，一组数据由多个特征和标签组成。当这些特征分别与标签存在线性关系的时候，我们就说这一组数据是线性数据。

但当我们在进行分类的时候，我们的数据分布往往是这样的：

这些数据都不能由一条直线来进行拟合，他们也没有均匀分布在某一条线的周围，那我们怎么判断，这些数据是线性数据还是非线性数据呢？在这里就要注意了，当我们在回归中绘制图像时，绘制的是特征与标签的关系图，横坐标是特征，纵坐标是标签，我们的标签是连续型的，所以我们可以通过是否能够使用一条直线来拟合图像判断数据究竟属于线性还是非线性。然而在分类中，我们绘制的是数据分布图，横坐标是其中一个特征，纵坐标是另一个特征，标签则是数据点的颜色。因此在分类数据中，我们使用“是否线性可分”（linearly separable）这个概念来划分分类数据集。当分类数据的分布上可以使用一条直线来将两类数据分开时，我们就说数据是线性可分的。反之，数据不是线性可分的。 ps：上面那张图我也不知道是不是线性可分的，大家知道以下这个概念就好。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
rnd = np.random.RandomState(42) #设置随机数种子
X = rnd.uniform(-3, 3, size=100) #random.uniform，从输入的任意两个整数中取出size个随机数
#生成y的思路：先使用NumPy中的函数生成一个sin函数图像，然后再人为添加噪音
y = np.sin(X) + rnd.normal(size=len(X)) / 3 #random.normal，生成size个服从正态分布的随机数
#使用散点图观察建立的数据集是什么样子
plt.scatter(X, y,marker='o',c='k',s=20)
plt.show()
#为后续建模做准备：sklearn只接受二维以上数组作为特征矩阵的输入
X = X.reshape(-1, 1)
#使用原始数据进行建模
LinearR = LinearRegression().fit(X, y)
TreeR = DecisionTreeRegressor(random_state=0).fit(X, y)
#放置画布
fig, ax1 = plt.subplots(1)
#创建测试数据：一系列分布在横坐标上的点
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)
#将测试数据带入predict接口，获得模型的拟合效果并进行绘制
ax1.plot(line, LinearR.predict(line), linewidth=2, color='green',
label="linear regression")
ax1.plot(line, TreeR.predict(line), linewidth=2, color='red',
label="decision tree")
#将原数据上的拟合绘制在图像上
ax1.plot(X[:, 0], y, 'o', c='k')
#其他图形选项
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Result before discretization")
plt.tight_layout()
plt.show()

从图像上可以看出，线性回归无法拟合出这条带噪音的正弦曲线的真实面貌，只能够模拟出大概的趋势，而决策树却
通过建立复杂的模型将几乎每个点都拟合出来了。可见，使用线性回归模型来拟合非线性数据的效果并不好，而决策
树这样的模型却拟合得太细致，相比之下，还是决策树的拟合效果更好一些。线性模型可以用来拟合非线性数据，而非线性模型也可以用来拟合线性数据，更神奇的是，有的算法没有模型也可以处理各类数据，而有的模型可以既可以是线性，也可以是非线性模型。