朴素贝叶斯

发表于 更新于 分类于

贝叶斯的性质

关键概念

​ 联合概率：X取值为x和Y取值为y两个事件同时发生的概率，表示为P(X=x,Y=y)

​ 条件概率：在X取值为x的前提下，Y取值为y的概率。表示为P(Y=y|X=x)

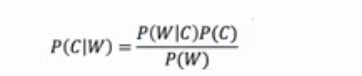
这里的C代表类别，W代表特征。

我们学习的其它分类算法总是有一个特点：这些算法先从训练集中学习，获取某种信息来建立模型，然后用模型去对测试集进行预测。比如逻辑回归，我们要先从训练集中获取让损失函数最小的参数，然后用参数建立模型，再对测试集进行预测。在比如支持向量机，我们要先从训练集中获取让边际最大的决策边界，然后 用决策边界对测试集进行预测。相同的流程在决策树，随机森林中也出现，我们在fit的时候必然已经构造好了能够让对测试集进行判断的模型。而朴素贝叶斯，似乎没有这个过程。这说明，朴素贝叶斯是一个不建模的算法。以往我们学的不建模算法，比如KMeans，比如PCA，都是无监督学习，而朴素贝叶斯是第一个有监督的，不建模的分类算法。我们认为，训练集和测试集都来自于同一个不可获得的大样本下，并且这个大样本下的各种属性所表现出来的规律应当是一致的，因此训练集上计算出来的各种概率，可以直接放到测试集上来使用。即便不建模，也可以完成分类。

sklearn中的朴素贝叶斯

sklearn中，基于高斯分布、伯努利分布、多项式分布为我们提供了四个朴素贝叶斯的分类器

高斯朴素贝叶斯

sklearnnaive_bayes.GaussianNB(priors=None,var_smoothing=1e-09)

高斯朴素贝叶斯，通过假设P(Xi|Y)是服从高斯分布(正态分布)，估计每个特征下每个类别上的条件概率。对于每个特征下的取值，有以下公式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
digits = load_digits()
X, y = digits.data, digits.target
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
gnb = GaussianNB().fit(Xtrain,Ytrain)
#查看分数
acc_score = gnb.score(Xtest,Ytest)
#查看预测结果
Y_pred = gnb.predict(Xtest)
#查看预测的概率结果
prob = gnb.predict_proba(Xtest)
print(prob)

概率类模型的评估指标

布里尔分数Brier Score　

概率预测的准确程度被称为“校准程度”，是衡量算法预测出的概率和真实结果的差异的一种方式。一种比较常用的指标叫做布里尔分数，它被计算为是概率预测相对于测试样本的均方误差，表示为：

其中N是样本数量，Pi为朴素贝叶斯预测出的概率，Oi是样本所对应的真实结果，只能取到0或者1，如果事件发生则为1，如果不发生则为0。这个指标衡量了我们的概率距离真实标签结果的差异，其实看起来非常像是均方误差。布里尔分数的范围是从0到1，分数越高则预测结果越差劲，校准程度越差，因此布里尔分数越接近0越好。由于它的本质也是在衡量一种损失，所以在sklearn当中，布里尔得分被命名为brier_score_loss。我们可以从模块metrics中导入这个分数来衡量我们的模型评估结果： 

1
2
3
4
5
#接上面的代码
from sklearn.metrics import brier_score_loss
#注意，第一个参数是真实标签，第二个参数是预测出的概率值
#我们的pos_label与prob中的索引一致，就可以查看这个类别下的布里尔分数是多少
print(brier_score_loss(Ytest, prob[:,1], pos_label=1))

对数似然函数

另一种常用的概率损失衡量是对数损失（log_loss），又叫做对数似然，逻辑损失或者交叉熵损失。由于是损失，因此对数似然函数的取值越小，则证明概率估计越准确，模型越理想。值得注意得是，对数损失只能用于评估分类型模型

在sklearn，我们可以从metrics模块中导入我们的对数似然函数：

1
2
from sklearn.metrics import log_loss
print(log_loss(Ytest,prob))

第一个参数是真实标签，第二个参数是我们预测的概率。真正的概率必须要以接口predict_proba来调用，千万避免混淆。

那什么时候使用对数似然，什么时候使用布里尔分数？

可靠性曲线

可靠性曲线（reliability curve），又叫做概率校准曲线（probability calibration curve），可靠性图（reliability
diagrams），这是一条以预测概率为横坐标，真实标签为纵坐标的曲线。我们希望预测概率和真实值越接近越好，
最好两者相等，因此一个模型/算法的概率校准曲线越靠近对角线越好。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import make_classification as mc
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import brier_score_loss
from sklearn.model_selection import train_test_split
X, y = mc(n_samples=100000,n_features=20 #总共20个特征
,n_classes=2 #标签为2分类
,n_informative=2 #其中两个代表较多信息
,n_redundant=10 #10个都是冗余特征
,random_state=42)
#样本量足够大，因此使用1%的样本作为训练集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, y,test_size=0.99,random_state=42)
gnb = GaussianNB()
gnb.fit(Xtrain,Ytrain)
y_pred = gnb.predict(Xtest)
prob_pos = gnb.predict_proba(Xtest)[:,1] #我们的预测概率 - 横坐标
clf_score=brier_score_loss(Ytest,prob_pos,pos_label=1)
#Ytest - 我们的真实标签 - 横坐标
#在我们的横纵表坐标上，概率是由顺序的（由小到大），为了让图形规整一些，我们要先对预测概率和真实标签按照预测
#概率进行一个排序，这一点我们通过DataFrame来实现
df = pd.DataFrame({"ytrue":Ytest[:500],"probability":prob_pos[:500]})
df = df.sort_values(by="probability")
df.index = range(df.shape[0])
#紧接着我们就可以画图了
fig = plt.figure()
ax1 = plt.subplot()
ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated") #得做一条对角线来对比呀
ax1.plot(df["probability"],df["ytrue"],"s-",label="%s (%1.3f)" % ("Bayes", clf_score))
ax1.set_ylabel("True label")
ax1.set_xlabel("predcited probability")
ax1.set_ylim([-0.05, 1.05])
ax1.legend()
plt.show()

为什么存在这么多上下穿梭的直线？因为我们是按照预测概率的顺序进行排序的，而预测概率从0开始到1的过程中，真实取值不断在0和1之间变化，而我们是绘制折线图，因此无数个纵坐标分布在0和1的被链接起来了，所以看起来如此混乱。那我们换成散点图来试试看呢？ 

1
2
3
4
5
6
7
8
9
10
#接上面的代码
fig = plt.figure()
ax1 = plt.subplot()
ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
ax1.scatter(df["probability"],df["ytrue"],s=10)
ax1.set_ylabel("True label")
ax1.set_xlabel("predcited probability")
ax1.set_ylim([-0.05, 1.05])
ax1.legend()
plt.show()

可以看到，由于真实标签是0和1，所以所有的点都在y=1和y=0这两条直线上分布，这完全不是我们希望看到的图像。回想一下我们的可靠性曲线的横纵坐标：横坐标是预测概率，而纵坐标是真实值，我们希望预测概率很靠近真实值，那我们的真实取值必然也需要是一个概率才可以，如果使用真实标签，那我们绘制出来的图像完全是没有意义的。但是，我们去哪里寻找真实值的概率呢？这是不可能找到的——如果我们能够找到真实的概率，那我们何必还用算法来估计概率呢，直接去获取真实的概率不就好了么？所以真实概率在现实中是不可获得的。但是，我们可以获得类概率的指标来帮助我们进行校准。一个简单的做法是，将数据进行分箱，然后规定每个箱子中真实的少数类所占的比例为这个箱上的真实概率trueproba，这个箱子中预测概率的均值为这个箱子的预测概率predproba，然后以trueproba为纵坐标，predproba为横坐标，来绘制我们的可靠性曲线。

在sklearn中，这样的做法可以通过绘制可靠性曲线的类calibration_curve来实现。和ROC曲线类似，类calibration_curve可以帮助我们获取我们的横纵坐标，然后使用matplotlib来绘制图像。该类有如下参数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#接上面的代码
from sklearn.calibration import calibration_curve
#从类calibiration_curve中获取横坐标和纵坐标
trueproba, predproba = calibration_curve(Ytest, prob_pos
,n_bins=10 #输入希望分箱的个数
)
fig = plt.figure()
ax1 = plt.subplot()
ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
ax1.plot(predproba, trueproba,"s-",label="%s (%1.3f)" % ("Bayes", clf_score))
ax1.set_ylabel("True probability for class 1")
ax1.set_xlabel("Mean predcited probability")
ax1.set_ylim([-0.05, 1.05])
ax1.legend()
plt.show()

根据不同的n_bins取值得出不同的曲线

1
2
3
4
5
6
7
8
9
10
11
12
#接上面的代码
fig, axes = plt.subplots(1,3,figsize=(18,4))
for ind,i in enumerate([3,10,100]):
    ax = axes[ind]
    ax.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
    trueproba, predproba = calibration_curve(Ytest, prob_pos,n_bins=i)
    ax.plot(predproba, trueproba,"s-",label="n_bins = {}".format(i))
    ax.set_ylabel("True probability for class 1")
    ax.set_xlabel("Mean predcited probability")
    ax.set_ylim([-0.05, 1.05])
    ax.legend()
plt.show()

很明显可以看出，n_bins越大，箱子越多，概率校准曲线就越精确，但是太过精确的曲线不够平滑，无法和我们希望的完美概率密度曲线相比较。n_bins越小，箱子越少，概率校准曲线就越粗糙，虽然靠近完美概率密度曲线，但是无法真实地展现模型概率预测地结果。因此我们需要取一个既不是太大，也不是太小的箱子个数，让概率校准曲线既不是太精确，也不是太粗糙，而是一条相对平滑，又可以反应出模型对概率预测的趋势的曲线。通常来说，建议先试试看箱子数等于10的情况。箱子的数目越大，所需要的样本量也越多，否则曲线就会太过精确。

校准可靠性曲线

sklearn中的概率校正类CalibratedClassifierCV来对二分类情况下的数据集进行概率校正

base_estimator

需要校准其输出决策功能的分类器，必须存在predict_proba或decision_function接口。 如果参数cv = prefit，分类
器必须已经拟合数据完毕。

cv

整数，确定交叉验证的策略。可能输入是：
None，表示使用默认的3折交叉验证。在版本0.20中更改：在0.22版本中输入“None”，将由使用3折交叉验证改为5折交叉验证

任意整数，指定折数对于输入整数和None的情况下来说，如果时二分类，则自动使用类sklearn.model_selection.StratifiedKFold进行折数分割。如果y是连续型变量，则使用sklearn.model_selection.KFold进行分割。

已经使用其他类建好的交叉验证模式或生成器cv。

可迭代的，已经分割完毕的测试集和训练集索引数组。

输入”prefit”，则假设已经在分类器上拟合完毕数据。在这种模式下，使用者必须手动确定用来拟合分类器的数
据与即将倍校准的数据没有交集

method

进行概率校准的方法，可输入”sigmoid”或者”isotonic”
输入’sigmoid’，使用基于Platt的Sigmoid模型来进行校准
输入’isotonic’，使用等渗回归来进行校准
当校准的样本量太少（比如，小于等于1000个测试样本）的时候，不建议使用等渗回归，因为它倾向于过拟合。样
本量过少时请使用sigmoids，即Platt校准。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import make_classification as mc
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import brier_score_loss
from sklearn.calibration import calibration_curve
from sklearn.linear_model import LogisticRegression as LR
from sklearn.model_selection import train_test_split
X, y = mc(n_samples=100000,n_features=20 #总共20个特征
,n_classes=2 #标签为2分类
,n_informative=2 #其中两个代表较多信息
,n_redundant=10 #10个都是冗余特征
,random_state=42)
#样本量足够大，因此使用1%的样本作为训练集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, y,test_size=0.99,random_state=42)
def plot_calib(models,name,Xtrain,Xtest,Ytrain,Ytest,n_bins=10):
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 6))
    ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
    for clf, name_ in zip(models, name):
        clf.fit(Xtrain, Ytrain)
        y_pred = clf.predict(Xtest)
    # hasattr(obj,name)：查看一个类obj中是否存在名字为name的接口，存在则返回True
        if hasattr(clf, "predict_proba"):
            prob_pos = clf.predict_proba(Xtest)[:, 1]
        else:  # use decision function
            prob_pos = clf.decision_function(Xtest)
            prob_pos = (prob_pos - prob_pos.min()) / (prob_pos.max() - prob_pos.min())
    # 返回布里尔分数
        clf_score = brier_score_loss(Ytest, prob_pos, pos_label=y.max())
        trueproba, predproba = calibration_curve(Ytest, prob_pos, n_bins=n_bins)
        ax1.plot(predproba, trueproba, "s-", label="%s (%1.3f)" % (name_, clf_score))
        ax2.hist(prob_pos, range=(0, 1), bins=n_bins, label=name_, histtype="step", lw=2)
    ax2.set_ylabel("Distribution of probability")
    ax2.set_xlabel("Mean predicted probability")
    ax2.set_xlim([-0.05, 1.05])
    ax2.legend(loc=9)
    ax2.set_title("Distribution of probablity")
    ax1.set_ylabel("True probability for class 1")
    ax1.set_xlabel("Mean predcited probability")
    ax1.set_ylim([-0.05, 1.05])
    ax1.legend()
    ax1.set_title('Calibration plots(reliability curve)')
    plt.show()
from sklearn.calibration import CalibratedClassifierCV
name = ["GaussianBayes","Logistic","Bayes+isotonic","Bayes+sigmoid"]
gnb = GaussianNB()
models = [gnb
 ,LR(C=1., solver='lbfgs',max_iter=3000,multi_class="auto")
#定义两种校准方式
,CalibratedClassifierCV(gnb, cv=2, method='isotonic')
,CalibratedClassifierCV(gnb, cv=2, method='sigmoid')]
if __name__=="__main__":
	plot_calib(models,name,Xtrain,Xtest,Ytrain,Ytest)

多项式朴素贝叶斯

在sklearn中，用来执行多项式朴素贝叶斯的类MultinomialNB包含如下的参数和属性：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from sklearn.preprocessing import MinMaxScaler
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
from sklearn.metrics import brier_score_loss
class_1 = 500
class_2 = 500 #两个类别分别设定500个样本
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [0.5, 0.5] #设定两个类别的方差
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False)
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y
,test_size=0.3
,random_state=420)
#先归一化，保证输入多项式朴素贝叶斯的特征矩阵中不带有负数
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
#先归一化，保证输入多项式朴素贝叶斯的特征矩阵中不带有负数
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
mnb = MultinomialNB().fit(Xtrain_, Ytrain)
mnb.predict(Xtest_)
mnb.predict_proba(Xtest_)
mnb.score(Xtest_,Ytest)
print(brier_score_loss(Ytest,mnb.predict_proba(Xtest_)[:,1],pos_label=1))

其实效果不是很理想，来试试看把Xtrain转换成分类型数据吧。注意我们的Xtrain没有经过归一化，因为做哑变量之后自然所有的数据就不会又负数了。看下面的代码：

1
2
3
4
5
6
7
from sklearn.preprocessing import KBinsDiscretizer
kbs = KBinsDiscretizer(n_bins=10, encode='onehot').fit(Xtrain)
Xtrain_ = kbs.transform(Xtrain)
Xtest_ = kbs.transform(Xtest)
mnb = MultinomialNB().fit(Xtrain_, Ytrain)
mnb.score(Xtest_,Ytest)
print(brier_score_loss(Ytest,mnb.predict_proba(Xtest_)[:,1],pos_label=1))

伯努利朴素贝叶斯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from sklearn.preprocessing import MinMaxScaler
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
from sklearn.metrics import brier_score_loss
class_1 = 500
class_2 = 500 #两个类别分别设定500个样本
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [0.5, 0.5] #设定两个类别的方差
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False)
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y
,test_size=0.3
,random_state=420)
#先归一化，保证输入多项式朴素贝叶斯的特征矩阵中不带有负数
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
from sklearn.naive_bayes import BernoulliNB
#普通来说我们应该使用二值化的类sklearn.preprocessing.Binarizer来将特征一个个二值化
#然而这样效率过低，因此我们选择归一化之后直接设置一个阈值
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
#不设置二值化
bnl_ = BernoulliNB().fit(Xtrain_, Ytrain)
bnl_.score(Xtest_,Ytest)
brier_score_loss(Ytest,bnl_.predict_proba(Xtest_)[:,1],pos_label=1)
#设置二值化阈值为0.5
bnl = BernoulliNB(binarize=0.5).fit(Xtrain_, Ytrain)
bnl.score(Xtest_,Ytest)
print(brier_score_loss(Ytest,bnl.predict_proba(Xtest_)[:,1],pos_label=1))

补集朴素贝叶斯

在sklearn中，补集朴素贝叶斯由类ComplementNB完成，它包含的参数和多项式贝叶斯也非常相似：

----本文结束，感谢您的阅读。如有错，请指正。----
大哥大嫂过年好！支持我一下呗
0%