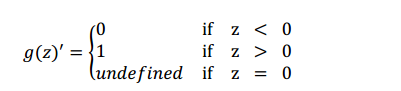本片博客介绍激活函数以及激活函数的作用。
首先激活函数是非线性连续的,激活函数有Sigmoid、tanh、Relu、Leaky Relu、Maxout、ELU。

激活函数(Activation functions)对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。其主要目的是将A-NN模型中一个节点的输入信号转换成一个输出信号。该输出信号现在被用作堆叠中下一个层的输入。
激活函数三问
问题一:为什么我们要使用激活函数呢?
如果不使用激活函数,我们的每一层输出只是承接了上一层输入函数的线性变换,无论神经网络有多少层,输出都是输入的线性组合。如果使用的话,激活函数给神经元引入了非线性的因素,使得神经网络可以逼近任何非线性函数,这样神经网络就可以应用到非线性模型中。
问题二:那么为什么我们需要非线性函数?
非线性函数是那些一级以上的函数,而且当绘制非线性函数时它们具有曲率。现在我们需要一个可以学习和表示几乎任何东西的神经网络模型,以及可以将输入映射到输出的任意复杂函数。神经网络被认为是通用函数近似器(Universal Function Approximators)。这意味着他们可以计算和学习任何函数。几乎我们可以想到的任何过程都可以表示为神经网络中的函数计算。
问题三:如何选择激活函数?
1、sigmoid 激活函数:除了输出层是一个二分类问题基本不会用它。
2、tanh 激活函数: tanh 是非常优秀的, 几乎适合所有场合。
3、ReLu 激活函数:最常用的默认函数,如果不确定用哪个激活函数,就使用 ReLu 或者Leaky ReLu。
常见激活函数
接下来介绍一下常用的激活函数:
sigmoid
该函数是将取值为 (−∞,+∞)的数映射到 (0,1) 之间。sigmoid函数的公式以及图形如下:
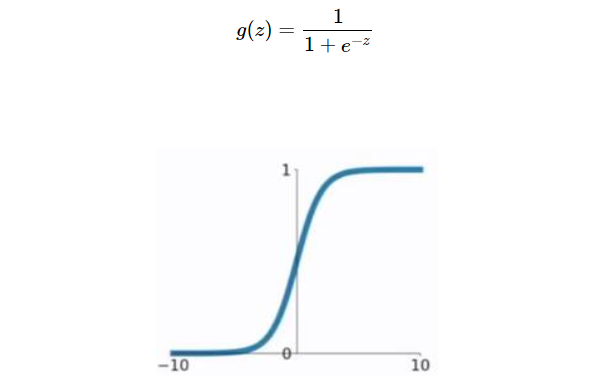
缺点:当 z 值非常大或者非常小时,通过上图我们可以看到,sigmoid函数的导数 g′(z)将接近 0 。这会导致权重 W 的梯度将接近 0 ,使得梯度更新十分缓慢,即梯度消失
tanh
该函数是将取值为 (−∞,+∞) 的数映射到(−1,1) 之间,其公式与图形为:
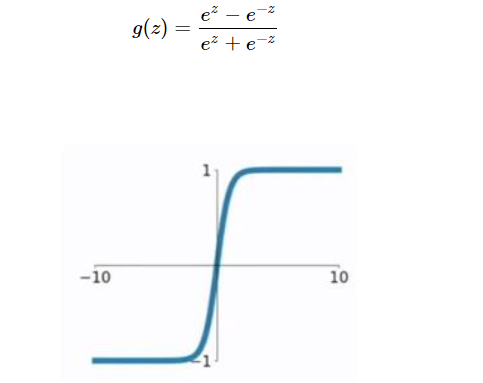
tanh函数的缺点同sigmoid函数的第一个缺点一样,当 z 很大或很小时,g′(z)接近于 0 ,会导致梯度很小,权重更新非常缓慢,即梯度消失问题。因此再介绍一个机器学习里特别受欢迎的激活函数 Relu函数。
Relu函数
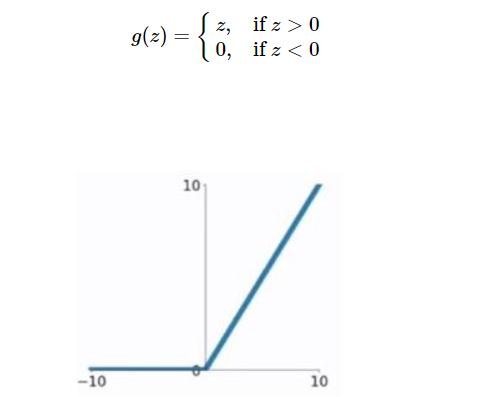
只要z是正值的情况下,导数恒等于 1,当z是负值的时候,导数恒等于 0。z 等于0的时候没有导数,但是我们不需要担心这个点,假设其导数是0或者1即可。
激活函数选择的经验:如果输出是0和1的二分类问题,则输出层选择 sigmoid 函数,其他层选择 Relu 函数
Leaky Relu
这是一种对ReLU函数改进的函数,又称为PReLU函数,但其并不常用。其公式与图形如下:
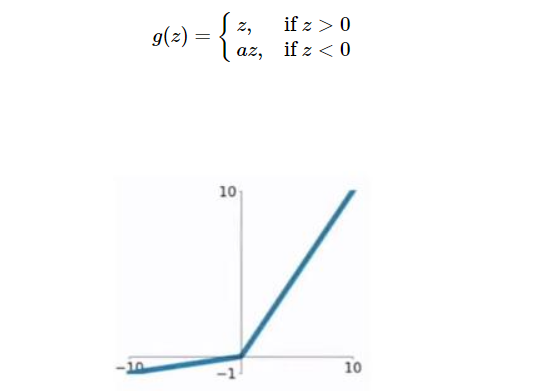
其中a取值在(0,1)之间
总结一下Relu 激活函数的优点:
Relu 函数在 z>0 的部分的导数值都大于0,并且不趋近于0,因而梯度下降速度较快。
Relu 函数在 z<0 的部分的导数值都等于0,此时神经元(就是模型中的圆圆)就不会得到训练,产出所谓的稀疏性,降低训练出来的模型过分拟合的概率。但即使这样,也有足够多的神经元使得 z>0。
激活函数的导数
在进行神经网络反向传播的时候,需要计算激活函数的斜率或者导数
sigmoid的求导
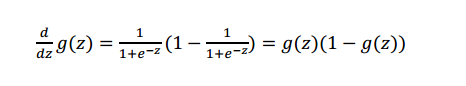
或者让 a=g(z),得
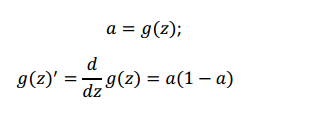
tanh的求导

我们同样让a=g(z),得
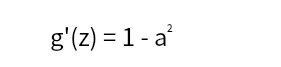
Relu的求导